题目内容
已知函数 (
( 为常数,
为常数, 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与 轴平行.
轴平行.
(Ⅰ)求 的值;
的值;
(Ⅱ)求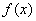 的单调区间;
的单调区间;
(Ⅲ)设 ,其中
,其中 为
为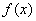 的导函数.
的导函数.
证明:对任意 .
.
解:(Ⅰ) ,依题意,
,依题意, 为所求.
为所求.
(Ⅱ)此时
 ,记
,记 ,
, ,所以
,所以 在
在 ,
, 单减,又
单减,又 ,
,
所以,当 时,
时, ,
, ,
, 单增;
单增;
当  时,
时, ,
, ,
, 单减.
单减.
所以,增区间为(0,1);减区间为(1, .
.
(Ⅲ) ,先研究
,先研究 ,再研究
,再研究 .
.
① 记 ,
, ,令
,令 ,得
,得 ,
,
当 ,
, 时,
时, ,
, 单增;
单增;
当 ,
, 时,
时, ,
, 单减 .
单减 .
所以, ,即
,即 .
.
② 记 ,
, ,所以
,所以 在
在 ,
, 单减,
单减,
所以, ,即
,即
综①、②知, .
.

练习册系列答案
相关题目
 则p是q成立的( )
则p是q成立的( ) +
+ 的最小值为( )
的最小值为( ) C.5 D.7
C.5 D.7 的图象可能是( )
的图象可能是( )

 .
. ,使得m[f(x)+
,使得m[f(x)+ ]+2=0恒成立,求实数m的取值范围.
]+2=0恒成立,求实数m的取值范围. x+
x+


 .-1或3
.-1或3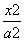
 -
-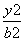 =1的焦距为10,点P(2,1)在C 的渐近线上,则C的方程为( )
=1的焦距为10,点P(2,1)在C 的渐近线上,则C的方程为( ) -
- =1 B.
=1 B. -
- =1
=1 -
- -
- =1
=1