题目内容
15.在△ABC中,$AB=AC=1,\overrightarrow{AM}=\overrightarrow{MB},\overrightarrow{BN}=\overrightarrow{NC},\overrightarrow{CM•}\overrightarrow{AN}=-\frac{1}{4}$,则∠ABC=( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 由题意画出图形,利用已知条件求出∠BAC=$\frac{π}{2}$,可得∠ABC=$\frac{π}{4}$.
解答 解:如图,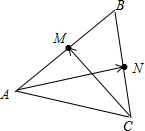
∵$AB=AC=1,\overrightarrow{AM}=\overrightarrow{MB},\overrightarrow{BN}=\overrightarrow{NC},\overrightarrow{CM•}\overrightarrow{AN}=-\frac{1}{4}$,
∴$\overrightarrow{CM}•\overrightarrow{AN}=(\overrightarrow{AM}-\overrightarrow{AC})•\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$=$(\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AC})•\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$
=$\frac{1}{4}|\overrightarrow{AB}{|}^{2}+\frac{1}{4}\overrightarrow{AB}•\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}•\overrightarrow{AC}-\frac{1}{2}|\overrightarrow{AC}{|}^{2}$
=$\frac{1}{4}-\frac{1}{4}cos∠BAC-\frac{1}{2}$=$-\frac{1}{4}$,解得cos∠BAC=0,
则∠BAC=$\frac{π}{2}$,
∴∠ABC=$\frac{π}{4}$.
故选:C.
点评 本题考查平面向量的数量积运算,考查了向量加法、减法的三角形法则,是中档题.

| A. | $-\frac{{\sqrt{5}}}{3}$ | B. | $-\frac{1}{3}$ | C. | $±\frac{2}{3}$ | D. | $\frac{2}{3}$ |
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |