题目内容
设△ABC的内角A、B、C所对边的长分别为a、b、c，且
+
=0
（Ⅰ）证明：c=3a；
（Ⅱ）若B为钝角，且b=20，求a的取值范围．
| cosA-3cosC |
| a-3c |
| cosB |
| b |
（Ⅰ）证明：c=3a；
（Ⅱ）若B为钝角，且b=20，求a的取值范围．
考点：余弦定理,正弦定理
专题：解三角形
分析：（Ⅰ）由条件利用正弦定理、两角和的正弦公式、求导公式，求得sinC=3sinA，可得c=3a．
（Ⅱ）由条件及余弦定理可得 cosB=
=
＜0，由此求得a的取值范围．
（Ⅱ）由条件及余弦定理可得 cosB=
| a2+c2-b2 |
| 2ac |
| 10a2-400 |
| 6a2 |
解答：
（Ⅰ）证明：在△ABC中，∵
+
=0，故由正弦定理可得
=-
，即化简可得sinBcosA-3sinBcosC=-sinAcosB+3sinCcosB，
∴sin（A+B）=3sin（B+C），即 sinC=3sinA，∴c=3a．
（Ⅱ）若B为钝角，且b=20，则由余弦定理可得 cosB=
=
＜0，
∴a2＜40，0＜a＜2
，即a的取值范围为（0，2
）．
| cosA-3cosC |
| a-3c |
| cosB |
| b |
| cosA-3cosC |
| sinA-3sinC |
| cosB |
| sinB |
∴sin（A+B）=3sin（B+C），即 sinC=3sinA，∴c=3a．
（Ⅱ）若B为钝角，且b=20，则由余弦定理可得 cosB=
| a2+c2-b2 |
| 2ac |
| 10a2-400 |
| 6a2 |
∴a2＜40，0＜a＜2
| 10 |
| 10 |
点评：本题主要考查正弦定理和余弦定理的应用，两角和的正弦公式，属于基础题．
练习册系列答案
相关题目
已知f（x）=ax3+bx2+cx是定义在[a-1，2a]上的奇函数，则a+b=（ ）
A、-
| ||
B、
| ||
C、
| ||
D、-
|
从5名同学中选3人参加某项会议，则选法种数为（ ）
| A、15 | B、10 | C、20 | D、60 |
任意向量
=（a1，a2），
=（b1，b2），定义运算?：
?
=（a2b2，a1b1），下列等式中（“+”和“•”是通常的向量加法和数量积，λ∈R），不恒成立的是（ ）
| a |
| b |
| a |
| b |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、（λ
| ||||||||||||||
D、
|
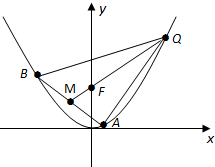已知抛物线C：x2=2py，的焦点为F，△ABQ的三个顶点都在抛物线C上，点M为AB的中点，