题目内容
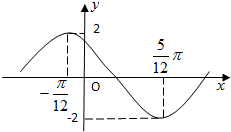
已知函数f(x)=Asin(ωx+ϕ)的导函数f′(x)在一个周期内的图象如右图,则下列函数f(x)的解析式中,满足条件的是( )
A.y=sin(2x+
| B.y=sin(2x+
| ||||
C.y=2sin(2x+
| D.y=2sin(2x+
|

由题意以及导函数的图象可知,函数f(x)=Asin(ωx+ϕ)的导函数f′(x)=Aωcos(ωx+ϕ),
Aω=2,T=2×(
+
)=π,所以ω=2,所以A=1
因为导函数的图象经过(-
,2),
所以2=2cos(2×(-
)+ϕ),
所以-
+ϕ=kπ,k∈Z,
当k=0时,ϕ=
.
所以函数的解析式为y=sin(2x+
)
故选A.
Aω=2,T=2×(
| 5π |
| 12 |
| π |
| 12 |
因为导函数的图象经过(-
| π |
| 12 |
所以2=2cos(2×(-
| π |
| 12 |
所以-
| π |
| 6 |
当k=0时,ϕ=
| π |
| 6 |
所以函数的解析式为y=sin(2x+
| π |
| 6 |
故选A.

练习册系列答案
相关题目
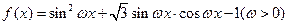 的周期为
的周期为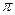 .
.
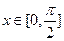 时,求
时,求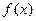 的取值范围;
的取值范围;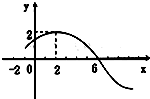


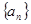 满足:
满足: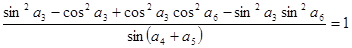 ,公差
,公差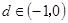 .若当且仅当
.若当且仅当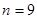 时,数列
时,数列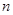 项和
项和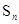 取得最大值,则首项
取得最大值,则首项 的取值范围是( ).
的取值范围是( ).


