题目内容
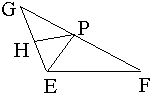 21、已知|
21、已知|| EF |
| EF |
| EH |
| EG |
| EO |
| EF |
| HP |
| EG |
(1)建立适当的平面直角坐标系,求出点P的轨迹方程;
(2)若点P的轨迹上存在两个不同的点A、B,且线段AB的中垂线与EF(或EF的延长线)有唯一的交点C,证明:|
| OC |
| c2 |
| a |
分析:(1)根据向量式转化成:|PE|+|PF|=|PG|+|PF|=|FG|=2a(>|EF|),结合椭圆的定义得点P的轨迹为椭圆,最后写出轨迹方程即可;
(2)先设A(x1,y1),B(x2,y2).A,B的中点M(x0,y0),C(t,0).分类讨论:①当kCM不存在时,显然成立.
②当kCM存在时,利用“点差法”得直线AB的斜率,再结合题中条件:“kAB•kCM=-1.”即可证得结论.
(2)先设A(x1,y1),B(x2,y2).A,B的中点M(x0,y0),C(t,0).分类讨论:①当kCM不存在时,显然成立.
②当kCM存在时,利用“点差法”得直线AB的斜率,再结合题中条件:“kAB•kCM=-1.”即可证得结论.
解答:解:(1)|PE|+|PF|=|PG|+|PF|=|FG|=2a(>|EF|),∴点P的轨迹为椭圆
∴轨迹方程为
+
=1
(2)设A(x1,y1),B(x2,y2).A,B的中点M(x0,y0),C(t,0).
当kCM不存在时,显然成立.
当kCM存在时,kCM=
.由“点差法”得:kAB=-
•
∵kAB•kCM=-1.x0=
∵|x0|<a∴|
|<a∴|t|<
即|
|<
.
∴轨迹方程为
| x2 |
| a2 |
| y2 |
| a2-c2 |
(2)设A(x1,y1),B(x2,y2).A,B的中点M(x0,y0),C(t,0).
当kCM不存在时,显然成立.
当kCM存在时,kCM=
| y0 |
| x0-t |
| a2-c2 |
| a2 |
| x0 |
| y0 |
∵kAB•kCM=-1.x0=
| a2-t |
| c2 |
| a2-t |
| c2 |
| c2 |
| a |
| OC |
| c2 |
| a |
点评:本小题主要考查椭圆的应用、轨迹方程、不等式的解法等基础知识,考查运算求解能力,解答的关键是利用设而不求的方法:“点差法”.

练习册系列答案
相关题目
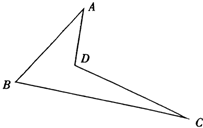 如图,已知空间四边形ABCD中,
如图,已知空间四边形ABCD中,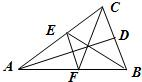 已知D、E、F分别是△ABC的边BC、CA、AB的中点,且
已知D、E、F分别是△ABC的边BC、CA、AB的中点,且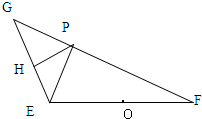 如图,已知
如图,已知 如图,已知
如图,已知