题目内容
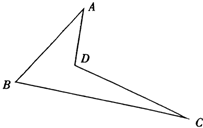如图，已知空间四边形ABCD中，| AB |
| a |
| c |
| CD |
| a |
| b |
| c |
| EF |
| a |
| b |
| c |
分析：把
分解为用已知向量表示的形式，可作图帮助分析已知向量与未知向量之间的关系，要注意中点向量表示中的特殊含意．
| EF |
解答：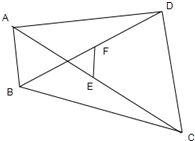
解：如图：
∵
=
+
+
，
又
=
+
+
，
两式相加，得
2
=（
+
）+（
+
）+（
+
）．
∵E是AC的中点，
故
+
=
．同理，
+
=
．
∴2
=
+
=（
-2
）+（5
+6
-8
）=6
+6
-10
．
∴
=3
+3
-5
．
故答案为：3
+3
-5
．
解：如图：∵
| EF |
| EA |
| AB |
| BF |
又
| EF |
| EC |
| CD |
| DF |
两式相加，得
2
| EF |
| EA |
| EC |
| AB |
| CD |
| BF |
| DF |
∵E是AC的中点，
故
| EA |
| EC |
| 0 |
| BF |
| DF |
| 0 |
∴2
| EF |
| AB |
| CD |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
∴
| EF |
| a |
| b |
| c |
故答案为：3
| a |
| b |
| c |
点评：本题考查的知识点是平面向量加（减）法的几何意义，处理的关键是：用已知向量表示未知向量的关键是将未知向量“凑配”成用已知向量表示的形式．其核心是向量加减法的“三角形”法则．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
如图，已知空间四边形ABCD的对角线AC=10，BD=6，M、N分别是AB、CD的中点，MN=7，求异面直线AC与BD所成的角．
如图，已知空间四边形ABCD中，AB=CD=3，E、F分别是BC、AD上的点，并且BE：EC=AF：FD=1：2，EF=
如图，已知空间四边形ABCD中，O是对角线BD的中点，