题目内容
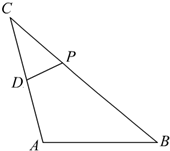如图，已知|| AB |
| BC |
| AD |
| 1 |
| 2 |
| AC |
| DP |
| AC |
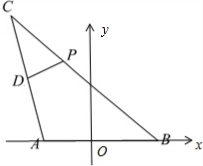
（1）建立适当的平面直角坐标系，求出点P的轨迹方程；
（2）若点P的轨迹上存在两个不同的点E、F，且线段EF的中垂线与AB（或AB的延长线）相交于一点Q，求出点Q的活动范围．
分析：（1）由已知，根据向量关系，结合线段中垂线性质，研究出|
+|
|=|
|=2a＞2c，得知点P是以A，B为焦点，长轴长为2a的椭圆，可写出其轨迹方程．
（2）设E（x1，y1），F（x2，y2），Q（x0，0），得出 x0=
，再根据-a≤x1≤a，-a≤x2≤a求出|x0|＜
．点在与AB中点相距
的线段上活动（不包括两端点）．
| PA| |
| PB |
| BC |
（2）设E（x1，y1），F（x2，y2），Q（x0，0），得出 x0=
| (x1+x2)c2 |
| 2a |
| c2 |
| a |
| c2 |
| a |
解答：解：如图，以A，B所在直线为x轴，A，B的中垂线为y轴，建立平面直角坐标系．由题设，2
=
，
•
=0，
∴||
|=
|．
而|
+|
|=|
|=2a＞2c
∴点P是以A，B为焦点，长轴长为2a的椭圆．即
+
=1
（2）设E（x1，y1），F（x2，y2），Q（x0，0）
x1≠x2，|
|=|
|
即（x1-x0）2+y12=（x2-x0）2+y22 ①
又E，F在轨迹上，∴
+
=1，
+
=1
将y12，y22 ，代入①式整理，得
2（x2-x1）═（x2-x1）2•
∵x1≠x2，∴x0=
-a≤x1≤a，-a≤x2≤a，
-2a＜x1+x2 ＜2a
-
＜x0＜
．
即|x0|＜
．
∴点在与AB中点相距
的线段上活动（不包括两端点）．
| AD |
| AC |
| PD |
| AC |
∴||
| PC |
| |PA |
而|
| PA| |
| PB |
| BC |
∴点P是以A，B为焦点，长轴长为2a的椭圆．即
| x2 |
| a2 |
| y2 |
| a2-c2 |
（2）设E（x1，y1），F（x2，y2），Q（x0，0）
x1≠x2，|
| QE |
| QF |
即（x1-x0）2+y12=（x2-x0）2+y22 ①
又E，F在轨迹上，∴
| x12 |
| a2 |
| y12 |
| a2-c2 |
| x22 |
| a2 |
| y22 |
| a2-c2 |
将y12，y22 ，代入①式整理，得
2（x2-x1）═（x2-x1）2•
| c2 |
| a2 |
∵x1≠x2，∴x0=
| (x1+x2)c2 |
| 2a |
-a≤x1≤a，-a≤x2≤a，
-2a＜x1+x2 ＜2a
-
| c2 |
| a |
| c2 |
| a |
即|x0|＜
| c2 |
| a |
∴点在与AB中点相距
| c2 |
| a |
点评：本题考查椭圆的定义、标准方程，椭圆的简单几何性质，直线与椭圆位置关系．（1）中得出而|
+|
|=|
|=2a＞2c （2）中得出 x0=
是关键．考查解析法的思想、计算能力．
| PA| |
| PB |
| BC |
| (x1+x2)c2 |
| 2a |
练习册系列答案
相关题目
如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB=2，F为CD的中点．
（2012•天津）如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于点D，过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF=3，FB=1，EF=
A：如图，已知AB是⊙O的直径，AC是弦，直线CE和⊙O切于点C，AD⊥CE，垂足为D．
（2012•河西区二模）如图，已知AB，CD是半径为a的圆O的两条弦，它们相交于AB的中点P，CP=
如图，已知AB⊥平面ACD，DE⊥平面ACD，且AC=AD=DE=2AB=4，F为CD的中点．