题目内容
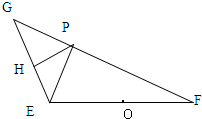 如图,已知|
如图,已知|| EF |
| FG |
| EH |
| EG |
| EO |
| EF |
| HP |
| EG |
(1)建立适当的平面直角坐标系,写出点P的轨迹方程;
(2)若点P的轨迹上存在两个不同的点A,B,且线段AB的中垂线与EF(或EF的延长线)相交于一点C,求证:|
| OC |
| c2 |
| a |
(3)若a
| OF |
| OM |
| OQ |
| QM |
分析:(1)以EF所在的直线为x轴,EF的中垂线为y轴,建立平面直角坐标系,利用向量的数量积可得|
|+|
|=|
|=2a,从而可得点P的轨迹是以E、F为焦点,长轴长为2a的椭圆,即可求轨迹方程;
(2)设出C的坐标,确定横坐标的范围,即可证得结论;
(3)设OQ所在直线为所在直线,与椭圆方程联立,利用
•
=0,即可求点P的轨迹的离心率e的取值范围.
| PF |
| PE |
| PG |
(2)设出C的坐标,确定横坐标的范围,即可证得结论;
(3)设OQ所在直线为所在直线,与椭圆方程联立,利用
| OQ |
| QM |
解答: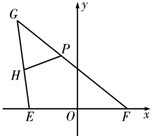 (1)解:如图,以EF所在的直线为x轴,EF的中垂线为y轴,建立平面直角坐标系.(1分)
(1)解:如图,以EF所在的直线为x轴,EF的中垂线为y轴,建立平面直角坐标系.(1分)
由题设2
=
,
•
=0,
∴|
|=|
|,而|
|+|
|=|
|=2a,
∴点P的轨迹是以E、F为焦点,长轴长为2a的椭圆,
故点P的轨迹方程是:
+
=1.(4分)
(2)证明:如图,设A(x1,y1),B (x2,y2),C (x0,0),
∴x1≠x2,且|
|=|
|,即(x1-x0)2+
=(x2-x0)2+
.①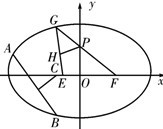
又A、B在轨迹上,∴
+
=1,
+
=1,
即
=a2-c2-
,
=a2-c2-
,(6分)
代入①整理得:2(x2-x1)•x0=
(
-
),(8分)
∵x1≠x2,∴x0=
.(8分)
∵-a≤x1≤a,-a≤x2≤a,∴-2a≤x1+x2≤2a.
∵x1≠x2,∴-2a<x1+x2<2a,
∴-
<x0<
,即|
|<
.(9分)
(3)解:由a
=c
,即点M为椭圆的右顶点,由
•
=0知直线OQ斜率必存在,
设OQ所在直线为所在直线为y=kx,
由
,解得
(其中b2=a2-c2) (11分)
∴
=(
,
)
=(a-
,
)
由
•
=0得
•(a-
)-
=0
化简得a=(1+k2)•
,(12分)
∴a2k2+b2=b2(1+k2)2
∴a2=2b2+b2k2≥2b2=2(a2-c2),
∴a2≤2c2,即
≤e<1
故离心率e的取值范围是[
,1)(14分)
 (1)解:如图,以EF所在的直线为x轴,EF的中垂线为y轴,建立平面直角坐标系.(1分)
(1)解:如图,以EF所在的直线为x轴,EF的中垂线为y轴,建立平面直角坐标系.(1分)由题设2
| EH |
| EG |
| HP |
| GE |
∴|
| PG |
| PE |
| PF |
| PE |
| PG |
∴点P的轨迹是以E、F为焦点,长轴长为2a的椭圆,
故点P的轨迹方程是:
| x2 |
| a2 |
| y2 |
| a2-c2 |
(2)证明:如图,设A(x1,y1),B (x2,y2),C (x0,0),
∴x1≠x2,且|
| CA |
| CB |
| y | 2 1 |
| y | 2 2 |

又A、B在轨迹上,∴
| ||
| a2 |
| ||
| a2-c2 |
| ||
| a2 |
| ||
| a2-c2 |
即
| y | 2 1 |
| a2-c2 |
| a2 |
| x | 2 1 |
| y | 2 2 |
| a2-c2 |
| a2 |
| x | 2 2 |
代入①整理得:2(x2-x1)•x0=
| c2 |
| a2 |
| x | 2 2 |
| x | 2 1 |
∵x1≠x2,∴x0=
| c2(x1+x2) |
| 2a2 |
∵-a≤x1≤a,-a≤x2≤a,∴-2a≤x1+x2≤2a.
∵x1≠x2,∴-2a<x1+x2<2a,
∴-
| c2 |
| a |
| c2 |
| a |
| OC |
| c2 |
| a |
(3)解:由a
| OF |
| OM |
| OQ |
| QM |
设OQ所在直线为所在直线为y=kx,
由
|
|
∴
| OQ |
| ab | ||
|
| abk | ||
|
| QM |
| ab | ||
|
| -abk | ||
|
由
| OQ |
| QM |
| ab | ||
|
| ab | ||
|
| a2b2k2 |
| a2k2+b2 |
化简得a=(1+k2)•
| ab | ||
|
∴a2k2+b2=b2(1+k2)2
∴a2=2b2+b2k2≥2b2=2(a2-c2),
∴a2≤2c2,即
| ||
| 2 |
故离心率e的取值范围是[
| ||
| 2 |
点评:本题考查轨迹方程,考查向量知识的运用,考查椭圆的几何性质,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.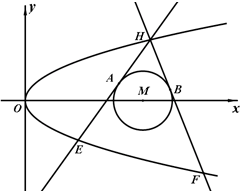 (2012•辽宁模拟)如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线与⊙M相切于A、两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为
(2012•辽宁模拟)如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线与⊙M相切于A、两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为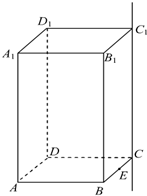 如图,已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,E为BC的中点,F为直线CC1上的动点,设
如图,已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,E为BC的中点,F为直线CC1上的动点,设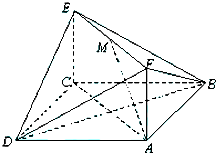 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=