题目内容
16.如图,在?ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{AO}$,$\overrightarrow{DB}$.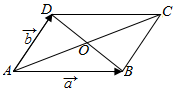
分析 根据向量数乘的几何意义和向量加法的平行四边形法则便可得出$\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{a}+\overrightarrow{b})$,而根据向量减法的几何意义即可用$\overrightarrow{a},\overrightarrow{b}$表示出向量$\overrightarrow{DB}$.
解答 解:$\overrightarrow{AO}=\frac{1}{2}\overrightarrow{AC}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD})=\frac{1}{2}(\overrightarrow{a}+\overrightarrow{b})$,$\overrightarrow{DB}=\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{a}-\overrightarrow{b}$.
点评 考查向量数乘的几何意义,向量减法的几何意义,以及向量加法的平行四边形法则.

练习册系列答案
相关题目
6.下列函数为偶函数的是( )
| A. | f(x)=x2-x | B. | f(x)=xcosx | C. | f(x)=xsinx | D. | $f(x)=1g({x+\sqrt{{x^2}+1}})$ |
7.从1、2、3、4、5这5个数中随机取出一个数,取出的数是某个整数的平方数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.等差数列-6,-1,4,9,…中的第20项为( )
| A. | 89 | B. | -101 | C. | 101 | D. | -89 |
1.下列函数为奇函数的是( )
| A. | y=2x-$\frac{1}{{2}^{x}}$ | B. | y=ln$\sqrt{1-{x}^{2}}$ | C. | y=x2-2x | D. | y=x2+2x |
6.已知集合A={y|y=|x|+1},B={x|x2≥1},则下列结论正确的是( )
| A. | -3∈A | B. | 3∉B | C. | A∩B=A | D. | A∪B=A |