题目内容
4.下列各式中,值为$\frac{{\sqrt{3}}}{2}$的是( )| A. | $\sqrt{\frac{{1+cos{{120}°}}}{2}}$ | B. | ${cos^2}\frac{π}{12}-{sin^2}\frac{π}{12}$ | ||
| C. | cos42°sin12°-sin42°cos12° | D. | $\frac{{tan{{15}°}}}{{1-{{tan}^2}{{15}°}}}$ |
分析 利用同角三角函数的基本关系式逐一化简四个选项得答案.
解答 解:∵$\sqrt{\frac{1+cos120°}{2}}$=$\sqrt{co{s}^{2}60°}=cos60°=\frac{1}{2}$;
$co{s}^{2}\frac{π}{12}-si{n}^{2}\frac{π}{12}=cos\frac{π}{6}=\frac{\sqrt{3}}{2}$;
cos42°sin12°-sin42°cos12°=sin(12°-42°)=-sin30$°=-\frac{1}{2}$;
$\frac{tan15°}{1-ta{n}^{2}15°}$=$\frac{1}{2}tan30°=\frac{\sqrt{3}}{6}$.
∴值为$\frac{{\sqrt{3}}}{2}$的是$co{s}^{2}\frac{π}{12}-si{n}^{2}\frac{π}{12}$.
故选:B.
点评 本题考查三角函数的化简与求值,考查了同角三角函数基本关系式的应用,是基础题.

练习册系列答案
相关题目
14.已知|$\overrightarrow{a}$|=10,|$\overrightarrow{b}$|=12,且$\overrightarrow{a}$•($\frac{1}{2}$$\overrightarrow{b}$)=-30,则$\overrightarrow{a}$和$\overrightarrow{b}$的夹角为( )
| A. | 60° | B. | 120° | C. | 135° | D. | 150° |
16.为了得到函数$y=sin(2x-\frac{π}{3})$的图象,只需把函数$y=cos(2x-\frac{π}{6})$的图象( )
| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{3}$个单位长度 | D. | 向右平移$\frac{π}{3}$个单位长度 |
13.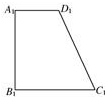 如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )
如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )
 如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )
如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )| A. | 12 | B. | 12$\sqrt{2}$ | C. | 24$\sqrt{2}$ | D. | 24 |
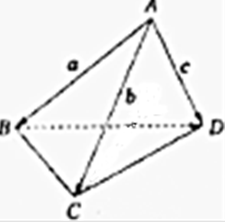 已知A、B、C、D是空间四个不同的点,求证:AC⊥BD的等价条件是AD2+BC2=CD2+AB2.
已知A、B、C、D是空间四个不同的点,求证:AC⊥BD的等价条件是AD2+BC2=CD2+AB2.