题目内容
14．
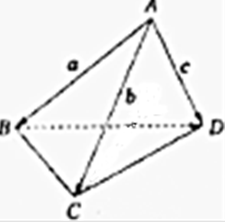已知A、B、C、D是空间四个不同的点，求证：AC⊥BD的等价条件是AD2+BC2=CD2+AB2．
分析 设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，$\overrightarrow{AD}$=$\overrightarrow{c}$，利用向量，求出相应的等价条件，即可得出结论．
解答 证明：设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，$\overrightarrow{AD}$=$\overrightarrow{c}$，则AC⊥BD的等价条件是$\overrightarrow{b}$•（$\overrightarrow{c}$-$\overrightarrow{a}$）=0，
∴$\overrightarrow{a}•\overrightarrow{b}$=$\overrightarrow{b}•\overrightarrow{c}$，
AD2+BC2=CD2+AB2，则$\overrightarrow{{c}^{2}}+（\overrightarrow{b}-\overrightarrow{a}）^{2}$=（$\overrightarrow{c}$-$\overrightarrow{b}$）2+$\overrightarrow{a}$2，
∴$\overrightarrow{a}•\overrightarrow{b}$=$\overrightarrow{b}•\overrightarrow{c}$，
∴AC⊥BD的等价条件是AD2+BC2=CD2+AB2．
点评 本题考查空间两条直线的位置关系，考查向量知识的运用，正确运用向量方法是关键．
| A． | $\sqrt{\frac{{1+cos{{120}°}}}{2}}$ | B． | ${cos^2}\frac{π}{12}-{sin^2}\frac{π}{12}$ | ||
| C． | cos42°sin12°-sin42°cos12° | D． | $\frac{{tan{{15}°}}}{{1-{{tan}^2}{{15}°}}}$ |