题目内容
6. 根据下面的要求,求1+3+5+…+99的值.
根据下面的要求,求1+3+5+…+99的值.(1)请完成执行该问题的程序框图;
(2)请用for语句写出该算法.
分析 (1)分析题目中的要求,发现这是一个累加型的问题,用循环结构来实现,在编写算法的过程中要注意,累加的初始值为0,累加值每一次增加2,退出循环的条件是i>100,把握住以上要点即可得解.
(2)根据流程图利用for语句可完成执行该问题的完整程序.
解答 解:(1)由题意,这是一个累加型的问题,用循环结构来实现,
由于累加的初始值为0,累加值每一次增加2,退出循环的条件是i>100,
故:①s=s+i;②i=i+2;③i≥100或i>99或(写一个即可)
(2)用for语句写出该算法如下:
s=0
For i=1 To 99 Step 2
s=s+i
Next
INPUT s
END
点评 本题考查了程序框图和伪代码.可利用循环语句来实现数值的累加(乘)常分如下步骤:①观察S的表达式分析,循环的初值、终值、步长②观察每次累加的值的通项公式③在循环前给累加器和循环变量赋初值,累加器的初值为0,累乘器的初值为1,环变量的初值同累加(乘)第一项的相关初值④在循环体中要先计算累加(乘)值,如果累加(乘)值比较简单可以省略此步,累加(乘),给循环变量加步长⑤输出累加(乘)值.属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
16.对某校高二年级某班63名同学,在一次期末考试中的英语成绩作统计,得到如下的列联表:
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,参照附表,得到的正确结论是( )
| 不低于120分(优秀) | 低于120分(非优秀) | |
| 男 | 12 | 21 |
| 女 | 11 | 19 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超过0.01的前提下认为“该班学生英语成绩优秀与性别有关” | |
| B. | 在犯错误的概率不超过0.05的前提下认为“该班学生英语成绩优秀与性别有关” | |
| C. | 没有90%以上的把握认为“该班学生英语成绩优秀与性别有关” | |
| D. | 有90%以上的把握认为“该班学生英语成绩优秀与性别有关” |
17.两个分类变量X与Y有关系的可能性越大,随机变量K2的值( )
| A. | 越大 | B. | 越小 | ||
| C. | 不变 | D. | 可能越大也可能越小 |
14.设ab<0,则下列四个式子:(1)|a-b|=|a|+|b|,(2)|a-b|<|a+b|,(3)|a+b|<|b|,(4)|a-b|>|a|-|b|中,正确的是( )
| A. | (1)、(2) | B. | (1)、(4) | C. | (3)、(4) | D. | (2)、(4) |
1.已知△ABC的平面直观图△A′B′C′,是边长为a的正三角形,那么原△ABC的面积为( )
| A. | $\frac{\sqrt{3}}{2}$a 2 | B. | $\frac{\sqrt{3}}{4}$a 2 | C. | $\frac{\sqrt{6}}{2}$a 2 | D. | $\sqrt{6}$a 2 |
11.在同一坐标系中,将曲线y=sinx通过φ:$\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}$变换后的曲线是( )
| A. | y'=3sin2x' | B. | y'=3sin$\frac{x'}{2}$ | C. | y'=$\frac{1}{3}$sin2x' | D. | y'=$\frac{1}{3}sin\frac{x'}{2}$ |
18.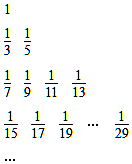 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
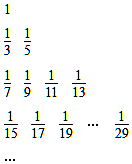 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )| A. | $\frac{1}{99}$ | B. | $\frac{1}{87}$ | C. | $\frac{1}{81}$ | D. | $\frac{1}{85}$ |
15.在极坐标系中,点$(4,\frac{π}{3})$到直线$ρsin(θ-\frac{π}{3})=2$的距离是( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | 1 |