题目内容
已知函数f(x)满足f(x)+1=
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]内,函数g(x)=f(x)-logm(x+2)有两个零点,则实数m的取值范围是( )
| 1 |
| f(x+1) |
A、(0,
| ||
B、(0,
| ||
| C、[3,+∞) | ||
| D、(1,3] |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:把函数的零点转化为两函数图象的交点,求出函数f(x)的解析式,利用数形结合即可得到结论.
解答:
解:∵f(x)+1=
,当x∈[0,1]时,f(x)=x,
∴x∈(-1,0)时,x+1∈(0,1),
则f(x)+1=
=
,
∴f(x)═
-1,
若函数g(x)=f(x)-logm(x+2)有两个零点,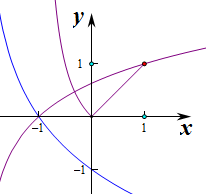
则由g(x)=f(x)-logm(x+2)=0
得f(x)=logm(x+2)有两个根,
即y=f(x)与y=g(x)=logm(x+2)的图象有两个交点,
函数图象如图,
当0<m<1时,函数y=logm(x+2)单调递减,此时不满足条件,
当m>1时,函数y=logm(x+2)单调递增,若两函数有两个交点,
则满足当x=1时,g(1)≤1,即logm3≤1,解得m≥3,
故选:C
| 1 |
| f(x+1) |
∴x∈(-1,0)时,x+1∈(0,1),
则f(x)+1=
| 1 |
| f(x+1) |
| 1 |
| x+1 |
∴f(x)═
| 1 |
| x+1 |
若函数g(x)=f(x)-logm(x+2)有两个零点,

则由g(x)=f(x)-logm(x+2)=0
得f(x)=logm(x+2)有两个根,
即y=f(x)与y=g(x)=logm(x+2)的图象有两个交点,
函数图象如图,
当0<m<1时,函数y=logm(x+2)单调递减,此时不满足条件,
当m>1时,函数y=logm(x+2)单调递增,若两函数有两个交点,
则满足当x=1时,g(1)≤1,即logm3≤1,解得m≥3,
故选:C
点评:本题考查了利用函数零点的存在性求变量的取值范围,考查了函数零点与函数图象与x轴的交点之间的关系,体现了数形结合的思想,和应用图象解决问题的能力.

练习册系列答案
相关题目
已知抛物线y2=4x的弦AB中点的横坐标为2,则|AB|的最大值为( )
| A、1 | B、3 | C、6 | D、12 |
如果椭圆
+
=1上一点P到它的右焦点距离是6,那么点P到它的左焦点的距离是( )
| x2 |
| 16 |
| y2 |
| 4 |
| A、2 | B、3 | C、4 | D、8 |
从932人中抽取一个样本容量为100的样本,采用系统抽样的方法则必须从这932人中剔除( )人.
| A、32 | B、24 | C、16 | D、48 |