题目内容
【题目】如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M. 
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连结AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】
(1)解:因为抛物线在x轴上的交点为B(1,0),和C(5,0),设抛物线的解析式为y=a(x﹣1)(x﹣5),
由抛物线过A(0,4),
∴a(0﹣1)(0﹣5)=4,
∴a= ![]() ,
,
∴抛物线解析式为y= ![]() (x﹣1)(x﹣5),即y=
(x﹣1)(x﹣5),即y= ![]() x2﹣
x2﹣ ![]() x+4,
x+4,
对称轴为直线x= ![]() =3
=3
(2)解:存在.如图所示,连接AC交对称轴于点P,连接BP,AB,

∵B,C关于对称轴对称,
AB+AP+PB=AB+AP+PC=AB+AC,
此时△PAB的周长最小,设直线AC方程为y=mx+n,将A(0,4),B(1,0),
代入可得 ![]() ,解得:
,解得:  ,即y=﹣
,即y=﹣ ![]() x+4,
x+4,
当x=3时,y=﹣ ![]() ×3+4=
×3+4= ![]() ,
,
∴P点坐标为(3, ![]() )
)
(3)解:存在.设N(t, ![]() t2﹣
t2﹣ ![]() t+4)(0<t<5),如图所示,过N作NF∥OA,分别交x轴和AC于F,G,
t+4)(0<t<5),如图所示,过N作NF∥OA,分别交x轴和AC于F,G,
过A作AD⊥FG的延长线于点D,连接CN,

根据(2)的AC解析式y=﹣ ![]() x+4,可得G(t,﹣
x+4,可得G(t,﹣ ![]() t+4),
t+4),
∴NG=﹣ ![]() t+4﹣(
t+4﹣( ![]() t2﹣
t2﹣ ![]() t+4)=﹣
t+4)=﹣ ![]() t2+4t,
t2+4t,
∵S△ANC=S△AGN+S△CGN,S△AGN= ![]() GN×AD,S△CGN=
GN×AD,S△CGN= ![]() CF×GN,
CF×GN,
∴S△ANC= ![]() GN×(AD+FC)=
GN×(AD+FC)= ![]() (﹣
(﹣ ![]() t2+4t)×5=﹣2t2+10t=﹣2(t﹣
t2+4t)×5=﹣2t2+10t=﹣2(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时△NAC的面积最大,最大值为
时△NAC的面积最大,最大值为 ![]() ,
,
此时 ![]() t2﹣
t2﹣ ![]() +4=
+4= ![]() ×(
×( ![]() )2﹣
)2﹣ ![]() ×
× ![]() +4=﹣3,
+4=﹣3,
∴此时N的坐标为( ![]() ,﹣3).
,﹣3).
【解析】(1)根据题意设抛物线的解析式为y=a(x﹣1)(x﹣5),再利用待定系数法即可求得抛物线的解析式.(2)根据两点之间线段最短可得到周长最短的情况,再根据已知两点求得直线解析式,即可求得所求点的坐标.(3)根据三角形的面积计算方法可以将三角形切割为两个便于计算的小三角形,再求每个三角形的底和高,即可表示出三角形的面积,根据二次函数的性质即可求得面积最大时的点的坐标.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.

【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为:
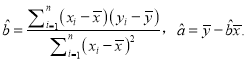
【题目】全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:
空气质量指数 |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 |
|
|
|
|
|
(1)根据所给统计表和频率分布直方图中的信息求出![]() 的值,并完成頻率分布直方图:
的值,并完成頻率分布直方图:
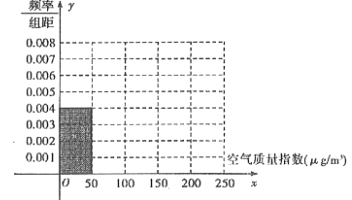
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,从中任意选取
天,从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.


