题目内容
20.程序框图如图所示:如果输入x=5,则输出结果为( )
| A. | 325 | B. | 109 | C. | 973 | D. | 295 |
分析 方法一:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算变量x的值,并输出.模拟程序的运行,用表格对程序运行过程中各变量的值进行分析,不难得到输出结果.
方法二:由程序框图可知:此问题相当于先求出满足以下条件:数列{an}的a1=5,an+1=3an-2,要求其通项公式第一次大于或等于200时即输出其值.
解答 解:方法一:程序在运行过程中各变量的值如下表示:
x 是否继续循环
循环前 5/
第一圈 13 是
第二圈 37 是
第三圈 109 是
第四圈 325 否
故最后输出的x值为325,
方法二:由序框图可知:此问题相当于先求出满足以下条件数列的通项公式,数列{an}的a1=5,an+1=3an-2,当an≥200时,即输出an.
∵an+1=3an-2,∴an+1-1=3(an-1),
∵a1-1=5-1=4≠0,∴数列{an}是以4为首项,3为公比的等比数列,
∴an-1=4×3n-1,
∴an=4×3n-1+1,
令4×3n-1+1≥200,解得n≥5.
故当n=5时,输出的x应是4×34+1=325.
选:A.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.

练习册系列答案
相关题目
8.设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为F1,F2,P是椭圆上的点.若PF1⊥F1F2,∠F1PF2=60°,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
12.已知函数f(x)满足f(1)=0,且f(x)在R上的导数满足f′(x)+1<0,则不等式f(x2)<-x2+1的解集为( )
| A. | (-∞,-1)∪(1,+∞) | B. | (1,+∞) | C. | (-∞,1) | D. | (-1,1 ) |
9.已知向量$\overrightarrow{a}$=(x1,y1,z1),$\overrightarrow{b}$=(x2,y2,z2),$\overrightarrow{a}$≠$\overrightarrow{b}$,设|$\overrightarrow{a}-\overrightarrow{b}$|=k,则|$\overrightarrow{a}-\overrightarrow{b}$与单位向量$\overrightarrow{i}$=(1,0,0)夹角的余弦值为( )
| A. | $\frac{{x}_{1}-{x}_{2}}{k}$ | B. | $\frac{{x}_{2}-{x}_{1}}{k}$ | C. | $\frac{|{x}_{1}-{x}_{2}|}{k}$ | D. | ±$\frac{{x}_{1}-{x}_{2}}{k}$ |
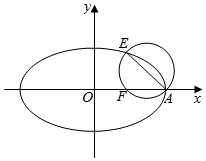 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆C过点$E(2e,\frac{b}{2})$,以AE为直径的圆恰好经过椭圆的右焦点F.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆C过点$E(2e,\frac{b}{2})$,以AE为直径的圆恰好经过椭圆的右焦点F.