题目内容
12．曲线y=x2 与直线y=x 所围成的封闭图形的面积为（ ）| A． | 1 | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{9}$ |
分析 利用定积分的几何意义，首先利用定积分表示面积，然后计算即可．
解答 解：曲线y=x2 与直线y=x 所围成的封闭图形的面积为${∫}_{0}^{1}（x-{x}^{2}）dx$=（$\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}$）|${\;}_{0}^{1}$=$\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$；
故选C．
点评 本题考查了定积分的几何意义的应用；关键是正确利用定积分表示面积．
练习册系列答案
相关题目
7．若锐角α满足cos（α+$\frac{π}{4}$）=$\frac{3}{5}$，则sin2α=（ ）
| A． | $\frac{7}{25}$ | B． | $\frac{16}{25}$ | C． | $\frac{18}{25}$ | D． | $\frac{24}{25}$ |
20．
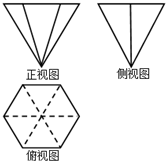一个几何体的三视图如图所示，其中正视图是边长为2的等边三角形，俯视图为正六边形，则该几何体的侧视图的面积是（ ）
一个几何体的三视图如图所示，其中正视图是边长为2的等边三角形，俯视图为正六边形，则该几何体的侧视图的面积是（ ）| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{3}{2}$ |
7．已知集合A={a，b}，B={c，d，e}，从A到B的不同映射个数是（ ）
| A． | 6 | B． | 8 | C． | 9 | D． | 5 |
1．如图所示，在四面体中，若直线EF和GH相交，则它们的交点一定（ ）
| A． | 在直线DB上 | B． | 在直线AB上 | C． | 在直线CB上 | D． | 都不对 |
2．为了得到函数y=sin（2x+$\frac{π}{3}$）的图象，只需将函数y=sinx的图象上所有的点（ ）
| A． | 横坐标伸长到原来的2倍，再向左平行移动$\frac{π}{3}$个单位长度 | |
| B． | 横坐标缩短到原来的$\frac{1}{2}$倍，再向左平行移动$\frac{π}{3}$个单位长度 | |
| C． | 横坐标缩短到原来的$\frac{1}{2}$倍，再向左平行移动$\frac{π}{6}$个单位长度 | |
| D． | 横坐标缩短到原来的$\frac{1}{2}$倍，再向右平行移动$\frac{π}{6}$个单位长度 |