题目内容
在极坐标系中，已知曲线C1：ρ＝12sinθ，曲线C2：ρ＝12cos
.
(1) 求曲线C1和C2的直角坐标方程；
(2) 若P、Q分别是曲线C1和C2上的动点，求PQ的最大值．
解：(1) 因为ρ＝12sinθ，所以ρ2＝12ρsinθ，所以x2＋y2－12y＝0，即曲线C1的直角坐标方程为x2＋(y－6)2＝36.又ρ＝12cos，所以ρ2＝12ρ
，所以x2＋y2－6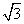
x－6y＝0，即曲线C2的直角坐标方程为(x－3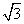)2＋(y－3)2＝36.
(2) PQmax＝6＋6＋
＝18.
练习册系列答案
相关题目
＝1在(x，y)→(x′，y′)＝(x＋2y，y)对应的变换下变换成另一个图形F′，试求F′的解析式．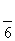
.
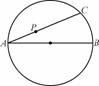
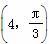，求|CP|.
