题目内容
17.韩国首尔医院近20天每天因患中东呼吸综合征而入院就诊的人数依次构成数列{an},己知a1=1,a2=2,且满足an+2-an=2+2(-1)n,n∈N+,则该医院20天内因患中东呼吸综合征就诊的人数共有210.分析 由an+2-an=2+2(-1)n,可得an+2-an=$\left\{\begin{array}{l}{0,n为奇数}\\{4,n为偶数}\end{array}\right.$,即n为奇数时,an+2=an,n为偶数时,an+2-an=4,即所有的奇数项都相等,所有的偶数项构成一个首项为2,公差为4的等差数列,根据a1=1,a2=2,可得a1=a3=…=a19=1,a2,a4,…,a20利用等差数列的求和公式求和,即可得到答案.
解答 解:an+2-an=2+2(-1)n,可得an+2-an=$\left\{\begin{array}{l}{0,n为奇数}\\{4,n为偶数}\end{array}\right.$,
即n为奇数时,an+2=an,n为偶数时,an+2-an=4,
∴a1=a3=…=a19,a2,a4,…,a20构成公差为4的等差数列,
∵a1=1,a2=2,
∴a1+a2+a3+a4+…+a19+a20=10+$20+\frac{10×9}{2}×4=210$.
故答案为:210.
点评 本题的考点是数列的应用,主要考查的数列的求和,由于已知的数列{an}即不是等差数列,又不是等比数列,故无法直接采用公式法,我们可以采用分组求和法,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.给出一个程序框图,则输出x的值是( )


| A. | 39 | B. | 41 | C. | 43 | D. | 45 |
12.已知全集U={x∈N*|x<9 },集合∁U(A∪B)={1,3},A∩∁UB={2,4},则集合B等于( )
| A. | {1,3,5,6,7,8} | B. | {2,4,5,6,7,8} | C. | {5,6,7,8} | D. | {1,2,3,4} |
9.已知函数f(x)=$\left\{{\begin{array}{l}{{{log}_2}x+a,x>0}\\{{2^x}+a,x≤0}\end{array}}$,若函数y=f(x)+x有且只有一个零点,则实数a的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,-1) | C. | (-1,+∞) | D. | [-1,+∞) |
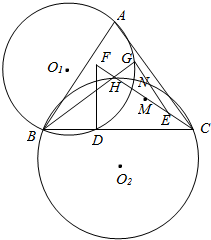 H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:
H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明: