题目内容
9.已知函数f(x)=$\left\{{\begin{array}{l}{{{log}_2}x+a,x>0}\\{{2^x}+a,x≤0}\end{array}}$,若函数y=f(x)+x有且只有一个零点,则实数a的取值范围是( )| A. | (-∞,-1] | B. | (-∞,-1) | C. | (-1,+∞) | D. | [-1,+∞) |
分析 根据题意可得,函数f(x)=$\left\{{\begin{array}{l}{{{log}_2}x+a,x>0}\\{{2^x}+a,x≤0}\end{array}}$的图象和直线y=-x有且只有一个交点,数形结合求得a的范围.
解答  解:由题意可得,函数f(x)=$\left\{{\begin{array}{l}{{{log}_2}x+a,x>0}\\{{2^x}+a,x≤0}\end{array}}$的图象和直线y=-x有且只有一个交点,如图所示:
解:由题意可得,函数f(x)=$\left\{{\begin{array}{l}{{{log}_2}x+a,x>0}\\{{2^x}+a,x≤0}\end{array}}$的图象和直线y=-x有且只有一个交点,如图所示:
故a<-1,
故选:B.
点评 本题主要考查方程根的存在性以及个数判断,体现了形结合、转化的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.按右图所示的程序框图运算,若输入 x=200,则输出 k 的值是( )
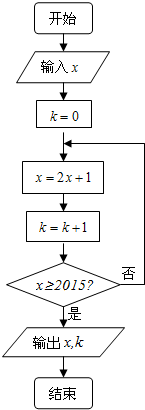

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
20.行如图所示的程序框图,若输入a=390,b=156,则输出a=( )
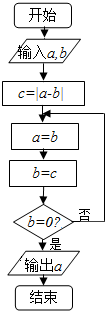

| A. | 26 | B. | 39 | C. | 78 | D. | 156 |
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线与圆x2+(y-3)2=1相切,则双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 3 |
14.已知集合M={x|x>1},N={x|-3<x<2},则集合M∩N等于( )
| A. | {x|-3<x<2} | B. | {x|-3<x<1} | C. | {x|1<x<2} | D. | {x|2<x<3} |
1.已知集合A={x|-1≤x≤1},B={x|x2-2x<0},则A∪(∁UB)=( )
| A. | [-1,0] | B. | [1,2] | C. | [0,1] | D. | (-∞,1]∪[2,+∞) |
19.下列各组函数中,表示同一函数的是( )
| A. | f(x)=$\sqrt{{x}^{2}}$,g(x)=($\sqrt{x}$)2 | B. | f(x)=(x-1)0,g(x)=1 | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=$\sqrt{{x}^{2}}$,g(t)=|t| |