题目内容
17.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F作直线y=-$\frac{b}{a}$x的垂线,垂足为A,交双曲线左支于B点,若$\overrightarrow{FB}$=2$\overrightarrow{FA}$,则该双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
分析 根据题意直线AB的方程为y=$\frac{a}{b}$(x-c)代入双曲线渐近线方程,求出A的坐标,进而求得B的表达式,代入双曲线方程整理求得a和c的关系式,进而求得离心率.
解答 解:设F(c,0),则直线AB的方程为y=$\frac{a}{b}$(x-c)代入双曲线渐近线方程y=-$\frac{b}{a}$x得A($\frac{{a}^{2}}{c}$,-$\frac{ab}{c}$),
由$\overrightarrow{FB}$=2$\overrightarrow{FA}$,可得B(-$\frac{{c}^{2}+2{a}^{2}}{3c}$,-$\frac{2ab}{3c}$),
把B点坐标代入双曲线方程$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
即$\frac{({c}^{2}+2{a}^{2})^{2}}{9{c}^{2}{a}^{2}}-\frac{4{a}^{2}}{9{c}^{2}}$=1,整理可得c=$\sqrt{5}$a,
即离心率e=$\frac{c}{a}$=$\sqrt{5}$.
故选:C.
点评 本题主要考查了双曲线的简单性质.解题的关键是通过分析题设中的信息,找到双曲线方程中a和c的关系.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
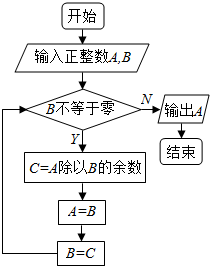
5.设有算法如图所示:如果输入A=225,B=135,则输出的结果是( )

| A. | 90 | B. | 45 | C. | 2 | D. | 0 |
6.已知A(1,2),B(3,7),$\overrightarrow{a}$=(x,-1),$\overrightarrow{AB}$∥$\overrightarrow{a}$,则( )
| A. | x=$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相同 | B. | x=-$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相同 | ||
| C. | x=$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相反 | D. | x=-$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相反 |
7.不等式(x-1)(x+2)≤0的解集为( )
| A. | (-2,1) | B. | [-2,1] | C. | (-∞,-2)∪(1,+∞) | D. | (-∞,-2]∪[1,+∞) |