题目内容
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)若![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②证明:对![]() ,
, ![]()
![]() .
.
(2)若![]() ,且对
,且对![]() ,有
,有![]() ,证明:
,证明:![]() .
.
【答案】(1)①![]() ;②证明见解析;(2)证明见解析
;②证明见解析;(2)证明见解析
【解析】
(1)①当![]() 时,
时,![]() ,两边取倒数,再根据数列递推关系,可得出数列
,两边取倒数,再根据数列递推关系,可得出数列![]() 是首项为2,公差为1的等差数列,即可求出数列
是首项为2,公差为1的等差数列,即可求出数列![]() 的通项公式;
的通项公式;
②由①知![]() ,利用裂项公式整理得出
,利用裂项公式整理得出![]() ,则对
,则对![]() ,根据裂项相消法即可求出
,根据裂项相消法即可求出![]() ;
;
(2)当![]() 时,
时,![]() ,则
,则![]() ,由于
,由于![]() ,则
,则![]() ,根据基本不等式得出
,根据基本不等式得出![]() ,化简整理有
,化简整理有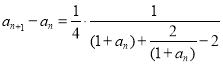 ,最后再利用基本不等式,即可证明出
,最后再利用基本不等式,即可证明出![]() .
.
解:(1)①当![]() 时,
时,![]() ,
,
∵![]() ,∴
,∴![]() ,依此类推,
,依此类推,![]()
∴![]() ,∴
,∴![]() ,
,
∴数列![]() 是首项为2,公差为1的等差数列,
是首项为2,公差为1的等差数列,
∴![]() ,即
,即![]() ,
,
②证明:由①知![]() ,故对
,故对![]()
![]() ,
,
∴![]()
=![]()
=![]() ,
,
(2)证明:当![]() 时,
时,![]() ,
,
则![]() ,
,
∵![]() ,则
,则![]() ,得
,得![]() ,
,
∴![]()
=![]()
=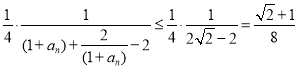 ,
,
∵![]() 与
与![]() 不能同时成立,所以上式“=”不成立,
不能同时成立,所以上式“=”不成立,
即对![]() ,
,![]() .
.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
【题目】某学校为了了解该校高三年级学生寒假在家自主学习的情况,随机对该校300名高三学生寒假的每天学习时间(单位:h)进行统计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图所示.
的分组作出频率分布直方图如图所示.

(Ⅰ)根据频率分布直方图计算该校高三年级学生的平均每天学习时间(同一组中的数据用该组区间中点值代表);
(Ⅱ)该校规定学习时间超过4h为合格,否则不合格.已知这300名学生中男生有140人,其中合格的有70人,请补全下表,根据表中数据,能否有99.9%的把握认为该校高三年级学生的性别与学习时长合格有关?
男生 | 女生 | 总计 | |
不合格 | |||
合格 | 70 | ||
总计 | 140 | 160 | 300 |
参考公式: ,其中
,其中![]() .
.
参考附表:
| 0.050 | 0.010 | 0.001 |
3.841 | 6.635 | 10.828 |