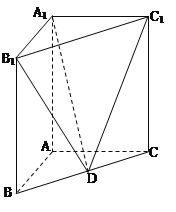
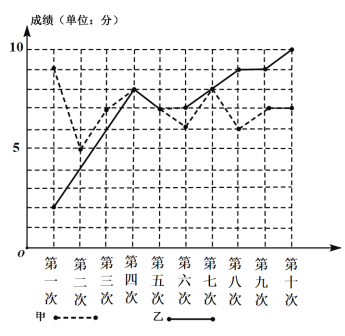
题目内容
【题目】(1)若![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的最大值
的最大值![]() ;
;
(2)在(1)的条件下,求证:函数![]() 在区间
在区间![]() 内存在唯一的极大值点
内存在唯一的极大值点![]() ,且
,且![]() .
.
【答案】(1)![]() .(2)家粘结性
.(2)家粘结性
【解析】
(1)令![]() ,求出导函数
,求出导函数![]() ,由
,由![]() 确定增区间,
确定增区间,![]() 确定减区间,从而得
确定减区间,从而得![]() 的最小值,得
的最小值,得![]() 的取值范围,即得
的取值范围,即得![]() ;
;
(2)求出导函数![]() ,通分后,令
,通分后,令![]() ,再求导数
,再求导数![]() ,令
,令![]() .分类讨论,当
.分类讨论,当![]() 时,
时,![]() ,得
,得![]() 递减,从而可得
递减,从而可得![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,
,![]() 时,令
时,令![]() .利用导数得
.利用导数得![]() 的单调性,从而得
的单调性,从而得![]() ,于是得出在
,于是得出在![]() 上
上![]() 的单调性,得唯一极大值点
的单调性,得唯一极大值点![]() .由
.由![]() 可对
可对![]() 变形,得
变形,得![]() ,只要证明在
,只要证明在![]() 上
上![]() ,从而可证得结论.
,从而可证得结论.
(1)解:令![]() ,则
,则![]() .
.
可见,![]() ;
;![]() .
.
故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以,当且仅当![]() 时,函数
时,函数![]() 取最小值1.
取最小值1.
由题意,实数![]() .所以
.所以![]() .
.
(2)由(1),![]() .
.
令![]() ,
,
则![]() .
.
令![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
可见,![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
又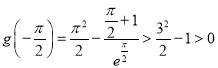 (由(1),可得
(由(1),可得![]() ,所以
,所以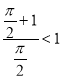 ),
),
![]() ,所以存在唯一的
,所以存在唯一的![]() ,使得
,使得![]() .
.
从而,当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减.
单调递减.
②当![]() 时,令
时,令![]() .
.
则![]() .所以
.所以![]() 在
在![]() 上单调递减.
上单调递减.
所以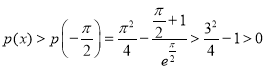 (由(1),可得
(由(1),可得![]() ,所以
,所以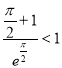 ).
).
又当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,从而
,从而![]() .所以
.所以![]() 在
在![]() 单调递增.
单调递增.
综上所述,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单词递减.
上单词递减.
所以,函数![]() 在区间
在区间![]() 内存在唯一极大值点
内存在唯一极大值点![]() .
.
关于![]() 的证明如下:
的证明如下:
由上面的讨论,![]() ,且
,且![]() ,所以
,所以![]() ,所以
,所以![]() .
.
于是![]() .
.
令![]() .当
.当![]() 时,
时,![]() .所以
.所以![]() 在
在![]() 上单调递增.所以,当
上单调递增.所以,当![]() 时,
时,![]() ,即
,即![]() .
.
又因为![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() .
.
所以![]() .
.

【题目】为了解某地网民浏览购物网站的情况,从该地随机抽取100名网民进行调查,其中男性、女性人数分别为60和40.下面是根据调查结果统计的数据,将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”,已知“网购达人”中女性人数为15人.
日均浏览购物网站时间(分钟) |
|
|
|
|
|
|
人数 | 2 | 14 | 24 | 35 | 20 | 5 |
(1)根据已知条件完成下面的![]() 列联表,并判断是否有99%的把握认为是否为“网购达人”与性别有关;
列联表,并判断是否有99%的把握认为是否为“网购达人”与性别有关;
非网购达人 | 网购达人 | 总计 | |
男 | |||
女 | 15 | ||
总计 |
(2)从上述调查中的“网购达人”中按性别分层抽样,抽取5人发放礼品,再从这5人中随机选出2人作为“最美网购达人”,求这两个“最美网购达人”中恰好为1男1女的概率.
参考公式: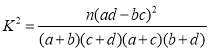 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |