题目内容
13.已知正数a,b,c满足约束条件:$\left\{\begin{array}{l}{a≤b+c}\\{a≥\frac{1}{3}(b+c)}\end{array}\right.$,且$\left\{\begin{array}{l}{b≤a+c}\\{b≥c-2a}\end{array}\right.$,则$\frac{2c-b}{a}$的最大值为( )| A. | $\frac{9}{2}$ | B. | $\frac{7}{2}$ | C. | 0 | D. | -1 |
分析 由题意得到关于$\frac{b}{a},\frac{c}{a}$的不等式组,令x=$\frac{b}{a}$,y=$\frac{c}{a}$换元后作出可行域,进一步求得目标函数z=$\frac{2c-b}{a}$=-x+2y的最大值.
解答 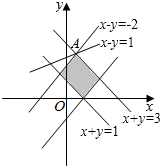 解:由$\left\{\begin{array}{l}{a≤b+c}\\{a≥\frac{1}{3}(b+c)}\end{array}\right.$,且$\left\{\begin{array}{l}{b≤a+c}\\{b≥c-2a}\end{array}\right.$,
解:由$\left\{\begin{array}{l}{a≤b+c}\\{a≥\frac{1}{3}(b+c)}\end{array}\right.$,且$\left\{\begin{array}{l}{b≤a+c}\\{b≥c-2a}\end{array}\right.$,
得$\left\{\begin{array}{l}{\frac{b}{a}+\frac{c}{a}≥1}\\{\frac{b}{a}+\frac{c}{a}≤3}\\{\frac{b}{a}-\frac{c}{a}≤1}\\{\frac{b}{a}-\frac{c}{a}≥-2}\end{array}\right.$,
令x=$\frac{b}{a}$,y=$\frac{c}{a}$,
则$\left\{\begin{array}{l}{x+y≥1}\\{x+y≤3}\\{x-y≤1}\\{x-y≥-2}\end{array}\right.$,z=$\frac{2c-b}{a}$=-x+2y.
作出可行域如图:
联立$\left\{\begin{array}{l}{x-y=-2}\\{x+y=3}\end{array}\right.$,解得A($\frac{1}{2},\frac{5}{2}$),
∴z=-x+2y的最大值为$\frac{9}{2}$.
故选:A.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
相关题目
3.已知一个四棱锥三视图如图所示,若此四棱锥的五个顶点在某个球面上,则该球的表面积为( )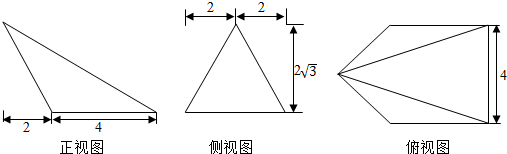

| A. | 48π | B. | 52π | C. | $\frac{172}{3}$π | D. | $\frac{196}{3}$π |
5.下列函数中既是奇函数,又是其定义域上的增函数的是( )
| A. | y=|x| | B. | y=lnx | C. | y=x${\;}^{\frac{1}{3}}$ | D. | y=x-3 |
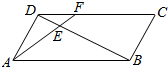 如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.
如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.