题目内容
已知函数
(1)若曲线 ,在点
,在点 处的切线与圆
处的切线与圆 相切,求
相切,求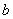 的取值范围;
的取值范围;
(2)若 ,讨论函数的单调性;
,讨论函数的单调性;
(3)证明:

 |
⑤

(3)由(2)可知:当b=1时,当x>1时,函数f(x)单调递减.
∴f(x)<f(1),即lnx﹣x2+x<0,令 ,可得
,可得 .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
已知函数
(1)若曲线 ,在点
,在点 处的切线与圆
处的切线与圆 相切,求
相切,求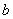 的取值范围;
的取值范围;
(2)若 ,讨论函数的单调性;
,讨论函数的单调性;
(3)证明:

 |
⑤

(3)由(2)可知:当b=1时,当x>1时,函数f(x)单调递减.
∴f(x)<f(1),即lnx﹣x2+x<0,令 ,可得
,可得 .
.


 名校课堂系列答案
名校课堂系列答案