题目内容
15.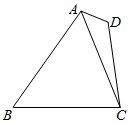 如图,在四边形ABCD中,△ACB与∠D互补,cos∠ACB=$\frac{1}{3}$,AC=BC=2$\sqrt{3}$,AB=4AD.
如图,在四边形ABCD中,△ACB与∠D互补,cos∠ACB=$\frac{1}{3}$,AC=BC=2$\sqrt{3}$,AB=4AD.(1)求AB的长;
(2)求sin∠ACD.
分析 (1)在△ABC中使用余弦定理求出AB;
(2)在△ACD中,使用正弦定理求出.
解答 解:(1)在△ABC中,由余弦定理得:
AB2=AC2+BC2-2AC•BCcos∠ACB=16.
∴AB=4.
(2)AD=$\frac{1}{4}AB$=1.
∵∠ACB与∠D互补,∴cosD=-cos∠ACB=-$\frac{1}{3}$.
∴sinD=$\frac{2\sqrt{2}}{3}$.
在△ACD中,由正弦定理得:$\frac{AC}{sinD}=\frac{AD}{sin∠ACD}$,
∴sin∠ACD=$\frac{AD•sinD}{AC}$=$\frac{2\sqrt{2}}{3×2\sqrt{3}}=\frac{\sqrt{6}}{9}$.
点评 本题考查了正弦定理,余弦定理解三角形,属于基础题.

练习册系列答案
相关题目
20.2015年,中国中国社科院发布《中国城市竞争力报告》公布了“中国十佳宜居城市”和“十佳最美丽城市”,如下表:
(I)记“中国十佳宜居城市”和“十佳最美丽城市”得分的平均数分别为$\overline{{x}_{1}}$与$\overline{{x}_{2}}$,方差分别为S12,S22,试比较
$\overline{{x}_{1}}$与$\overline{{x}_{2}}$,S12,S22的大小;(只需要写出结论)
(Ⅱ)旅游部门是从既要是“中国十佳宜居城市”又是“十佳最美丽城市”的城市中随机选取一个进行调研,求选到的城市两项排名的差的绝对值不大于3的概率;
(Ⅲ)某人计划外出旅游,因杭州,深圳,哈尔滨,烟台4所城市已经去过,准备从余下的“十佳最美丽城市”中随机选取2个游览,求选到的城市至少有一个是“中国十佳宜居城市”的概率.
| 2015年中国十佳宜居城市 | 2015年十佳最美丽城市 | ||||
| 排名 | 城市 | 得分 | 排名 | 城市 | 得分 |
| 1 | 深圳 | 90.2 | 1 | 杭州 | 93.7 |
| 2 | 珠海 | 89.8 | 2 | 拉萨 | 93.5 |
| 3 | 烟台 | 88.3 | 3 | 深圳 | 93.3 |
| 4 | 惠州 | 86.5 | 4 | 青岛 | 92.2 |
| 5 | 信阳 | 83.1 | 5 | 大连 | 92.0 |
| 6 | 厦门 | 81.4 | 6 | 银川 | 91.9 |
| 7 | 金华 | 79.2 | 7 | 惠州 | 90.6 |
| 8 | 柳州 | 77.8 | 8 | 哈尔滨 | 90.3 |
| 9 | 扬州 | 75.9 | 9 | 信阳 | 89.3 |
| 10 | 九江 | 74.6 | 10 | 烟台 | 88.8 |
$\overline{{x}_{1}}$与$\overline{{x}_{2}}$,S12,S22的大小;(只需要写出结论)
(Ⅱ)旅游部门是从既要是“中国十佳宜居城市”又是“十佳最美丽城市”的城市中随机选取一个进行调研,求选到的城市两项排名的差的绝对值不大于3的概率;
(Ⅲ)某人计划外出旅游,因杭州,深圳,哈尔滨,烟台4所城市已经去过,准备从余下的“十佳最美丽城市”中随机选取2个游览,求选到的城市至少有一个是“中国十佳宜居城市”的概率.
4.已知等比数列{an}中,an>0,a1+a2+…+a8=4,a1•a2…a8=16,则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{8}}$=( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
5.设0<a<1,0<b<1,曲线C1:y=ex+$\sqrt{a}$,C2:y=x+1+b,则曲线C1与C2有交点的概率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |