题目内容
5.已知向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(x,-1),且$\overrightarrow{a}-\overrightarrow{b}$与$\overrightarrow{b}$共线,则|x|的值为2.分析 由向量的坐标运算和平行关系可得x的方程,解方程可得.
解答 解:∵向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(x,-1),
∴$\overrightarrow{a}-\overrightarrow{b}$=(2-x,2),
∵$\overrightarrow{a}-\overrightarrow{b}$与$\overrightarrow{b}$共线,
∴-(2-x)=2x,
解得x=-2,故|x|=2
故答案为:2
点评 本题考查平行向量和共线向量,属基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
15.点P到图形C上所有点的距离的最小值称为点P到图形C的距离,那么平面内到定圆C的距离与到圆C外的定点A的距离相等的点的轨迹是( )
| A. | 射线 | B. | 椭圆 | C. | 双曲线的一支 | D. | 抛物线 |
20.直角三角形ABC,三内角成等差数列,最短边的边长为m(m>0),P是△ABC内一点,并且∠APB=∠APC=∠BPC=120°,则PA+PB+PC=$\sqrt{21}$时,m的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
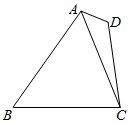 如图,在四边形ABCD中,△ACB与∠D互补,cos∠ACB=$\frac{1}{3}$,AC=BC=2$\sqrt{3}$,AB=4AD.
如图,在四边形ABCD中,△ACB与∠D互补,cos∠ACB=$\frac{1}{3}$,AC=BC=2$\sqrt{3}$,AB=4AD.