��Ŀ����
19������ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{r}^{2}-{a}^{2}}$=1�Ľ�����x���ϣ�F1��F2�ֱ�����Բ�����ҽ��㣬��P����Բ�ڵ�һ�����ڵĵ㣬ֱ��F2P��y�����Q������r=1ʱ��
��i������ԲE��������Ϊ$\frac{\sqrt{3}}{2}$������ԲE�ķ��̣�
��ii������P��ֱ��x+y=l��ʱ����ֱ��F1P��F1Q�ļнǣ�
����r=r0ʱ��������F1P��F1Q�����룺��a�仯ʱ����P�Ƿ���ij��ֱ���ϣ�����д����ֱ�߷��̣����������̣���
���� ����i����������Բ�������ʣ��Լ�b2=1-a2�����������ԲE�ķ��̣�
��ii����P��x0��y0����F1��-c��0����F2��c��0��������c$\sqrt{2{a}^{2}-1}$������б�ʵļ��㹫ʽ�͵�бʽ���ɵó�ֱ��F1P��б�ʣ�ֱ��F2P�ķ���Ϊб�ʣ�����б�ʳ˻�����-1��������нǣ�
�����ɣ�ii�������������PΪ��ֱ�ߣ�����Ϊx+y=r0��
��� �⣺����i����������b2=1-a2��c=$\sqrt{2{a}^{2}-1}$��$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$�����a2=$\frac{4}{5}$��b2=$\frac{1}{5}$��
������ԲE�ķ���Ϊ$\frac{5{x}^{2}}{4}$+5y2=1��
��ii����P��x0��y0����F1��-c��0����F2��c��0��������c=$\sqrt{2{a}^{2}-1}$��������֪x0��c��
��ֱ��y=1-x������ԲE�ķ��̣����ڵ�P����Բ�ڵ�һ�����ڵĵ㣬���x0=a2��y0=1-a2��
��ֱ��F1P��б��Ϊ$\frac{{y}_{0}}{{x}_{0}+c}$��ֱ��F2P��б��Ϊ$\frac{{y}_{0}}{{x}_{0}-c}$��
ֱ��F2P�ķ���Ϊy=$\frac{{y}_{0}}{{x}_{0}-c}$��x-c������x=0ʱ��y=$\frac{c{y}_{0}}{c-{x}_{0}}$
Q���������0��$\frac{c{y}_{0}}{c-{x}_{0}}$����
����ֱ��F1Q��б��Ϊ$\frac{{y}_{0}}{c-{x}_{0}}$��
����$\frac{{y}_{0}}{{x}_{0}+c}$•$\frac{{y}_{0}}{c-{x}_{0}}$=-1��
���� F1P��F1Q��
����ֱ��F1P��F1Q�ļн�Ϊ90�㣻
������PΪ��ֱ�ߣ�����Ϊx+y=r0��
�������£�
�ɣ�ii����֪��F1P��F1Q��
��$\frac{{y}_{0}}{{x}_{0}+c}$•$\frac{{y}_{0}}{c-{x}_{0}}$=-1��
����� y02=x02-��2a2-r0����
��Ϊ PΪ��ԲE�ϵ�һ�����ڵĵ㣬����ʽ����$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{r}^{2}-{a}^{2}}$=1
��x0=a2��y0=r0-a2��
����x0+y0=r0��
���Է���Ϊx+y=r0
���� ������Ҫ��������Բ�ı����̼��伸�����ʣ�ֱ�ߺ�ֱ�ߡ�ֱ�ߺ���Բ��λ�ù�ϵ�Ȼ���֪ʶ�ͻ������ܣ����������ν�ϵ�˼�롢���������ͼ����������������⣮

 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� ��ͼ��1����ʾ�����߶�BDΪֱ����Բ����A��C���㣬��AB=BC=1��BD=2���ӳ�DA��CB���ڵ�P������PAB��AB����ʹ��P����P��λ�õõ���ͼ2��ʾ�Ŀռ�ͼ�Σ����е�P����ƽ��ABCD�ڵ���ӰǡΪ�߶�AD���е�Q�����߶�P��B��P��C���е�ֱ�ΪE��F��
��ͼ��1����ʾ�����߶�BDΪֱ����Բ����A��C���㣬��AB=BC=1��BD=2���ӳ�DA��CB���ڵ�P������PAB��AB����ʹ��P����P��λ�õõ���ͼ2��ʾ�Ŀռ�ͼ�Σ����е�P����ƽ��ABCD�ڵ���ӰǡΪ�߶�AD���е�Q�����߶�P��B��P��C���е�ֱ�ΪE��F��

 ��ͼ������f��x����ͼ����P�㴦�����߷�����y=-2x+17������P�ĺ�������5����f��5��+f�䣨5��=��������
��ͼ������f��x����ͼ����P�㴦�����߷�����y=-2x+17������P�ĺ�������5����f��5��+f�䣨5��=��������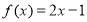 ��
�� ����
���� �Ľ���ʽ��_______.
�Ľ���ʽ��_______.