题目内容
4.在四棱锥P-ABCD中,底面ABCD是边长为10的正方形,若PD⊥平面ABCD,PD=AB.(I)求证:AC⊥PB.
(Ⅱ)求二面角A-PB-D的大小.
分析 (Ⅰ)连结AC,BD,交于点O,推导出AC⊥BD,AC⊥PD,从而AC⊥平面PBD,由此能证明AC⊥PB.
(2)过点A作AE⊥PB于E,连结EO,则∠AEO为二面角A-PB-D的平面角,由此能求出二面角A-PB-D的大小.
解答 证明:(Ⅰ)连结AC,BD,交于点O,
∵底面ABCD是正方形,∴AC⊥BD
又∵PD⊥平面ABCD,AC?平面ABCD,
∴AC⊥PD,
∵PD∩BD=D,∴AC⊥平面PBD,
∵PB?平面PBD,∴AC⊥PB
解:(2)过点A作AE⊥PB于E,连结EO,
由(1)可知AC⊥PB,∴PB⊥平面AEO,
∴∠AEO为二面角A-PB-D的平面角.
在Rt△PAB中,$AE=\frac{{10\sqrt{6}}}{3}$,
而由(1)知AC⊥平面PDB,AC⊥OE,
∴$sin∠AEO=\frac{AO}{AE}=\frac{{\sqrt{3}}}{2}$,∴∠AEO=60°,
故二面角A-PB-D为60°.
点评 本题考查线线垂直的证明,考查二面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
18.定积分${∫}_{0}^{π}$|sinx-cosx|dx的值是( )
| A. | 2+$\sqrt{2}$ | B. | 2-$\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
13.已知三次函数f(x)=ax3+x-b(a>0)在区间(0,1]内有零点,且f′(1)≤4,则f(-2)的取值范围是( )
| A. | (-10,-6) | B. | [-12,-2) | C. | [-12,-6) | D. | [-12,-10) |
16.已知某几何体的三视图如图所示,则该几何体的体积为( )
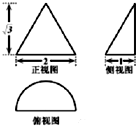

| A. | $\frac{\sqrt{3}π}{2}$ | B. | $\frac{\sqrt{3}π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{\sqrt{3}π}{6}$ |
12.一个空间几何体的三视图如图所示,则这个几何体的表面积为( )
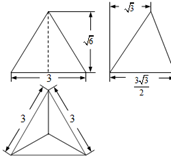

| A. | $\frac{{9\sqrt{3}}}{4}$ | B. | $9\sqrt{3}$ | C. | $\frac{{9\sqrt{2}}}{4}$ | D. | $9\sqrt{6}$ |