题目内容
乙.
(1)解:设等差数列{an}的公差为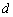 ,等比数列{bn}的公比为
,等比数列{bn}的公比为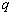 ,
,
依题意,得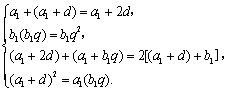 解得a1=d=1,b1=q=2.
解得a1=d=1,b1=q=2.
故an=n,bn=2n.…
(2)解:将a1,b1,b2记为第1组,a2,a3,a4,b3,b4,b5,b6记为第2组,a5,a6,a7,a8,a9,b7,b8,b9,b10,b11,b12记为第3组,……以此类推,则第n组中,有2n-1项选取于数列{an},有2 n项选取于数列{bn},前n组共有n2项选取于数列{an},有n2+n项选取于数列{bn},记它们的总和为Pn,并且有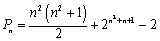 .
.
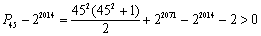 ,
,
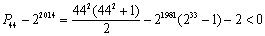 .
.
当 +(2+22+…+22012)时,
+(2+22+…+22012)时,
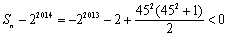 .当
.当 +(2+22+…+22013)时,
+(2+22+…+22013)时,
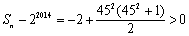 .
.
可得到符合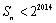 的最大的n=452+2012=4037.
的最大的n=452+2012=4037.

练习册系列答案
相关题目
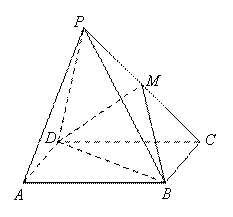
 (
( )的左焦点
)的左焦点 作
作 轴的垂线交椭圆于点
轴的垂线交椭圆于点 ,
, 为右焦点,若
为右焦点,若 ,则椭圆的离心率为( ).
,则椭圆的离心率为( ). B.
B. C.
C. D.
D.
 ,
, 满足
满足 则
则 的最大值是 .
的最大值是 . an(S4m+1)]=9,则
an(S4m+1)]=9,则 +
+ 的最小值是 .
的最小值是 . .
.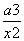 +1.
+1. =(1, x ),
=(1, x ), =(x-1, 2), 若
=(x-1, 2), 若