题目内容
已知a为实常数,y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,f(x)=2x-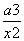 +1.
+1.
(1)求函数f(x)的单调区间;
(2)若f(x)≥a-1对一切x>0成立,求a的取值范围.
(1)解:由奇函数的对称性可知,我们只要讨论f(x)在区间(-∞,0)的单调性即可.
f ′(x)=2+ ,令f ′(x)=0,得x=-a.
,令f ′(x)=0,得x=-a.
①当a≤0时,f ′(x)>0,故f(x)在区间(-∞,0)是单调递增. …
②当a>0时,x ∈(-∞,-a ),f ′(x)>0,所以f(x)在区间(-∞,-a )是单调递增.
x ∈(-a,0),f ′(x)<0,所以f(x)在区间(-a,0)是单调减.
综上所述:当a≤0时,f(x)单调增区间为(-∞,0),(0,+∞);当a>0时,f(x)单调增区间为(-∞,-a ),(a ,+∞),单调减区间为(-a,0),(0,a).
(2)解:因为f(x)为奇函数,
所以当x>0时,f(x)=-f(-x)=-(-2 x-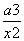 +1)=2x+
+1)=2x+ 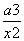 -1.
-1.
①当a<0时,要使f(x)≥a-1对一切x>0成立,即2x+ 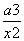 ≥a对一切x>0成立.
≥a对一切x>0成立.
而当x=- >0时,有-a+4a≥a,所以a≥0,则与a<0矛盾.
>0时,有-a+4a≥a,所以a≥0,则与a<0矛盾.
所以a<0不成立.
②当a=0时,f(x)=2x-1>-1=a-1对一切x>0成立,故a=0满足题设要求.
③当a>0时,由(1)可知f(x)在(0,a)是减函数,在(a ,+∞)是增函数.
所以 fmin(x)=
fmin(x)= f(a)=3a-1>a-1,所以a>0时也满足题设要求.
f(a)=3a-1>a-1,所以a>0时也满足题设要求.
综上所述,a的取值范围是 .
.

练习册系列答案
相关题目
 中,
中, ,
,
 ,设
,设 .
. 是等比数列;
是等比数列; 的前
的前 项和
项和 ;
; ,
, 为数列
为数列 的前
的前 的最大的整数.
的最大的整数. ,
, 满足
满足 则
则 的最大值是 .
的最大值是 .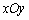 中,直线
中,直线 是曲线
是曲线 的切线,则当
的切线,则当 >0时,实数
>0时,实数 的最小值是 .
的最小值是 . ,
, 满足
满足 ,
, ,求
,求 .
. 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最小值为
的最小值为 B.
B. C.
C. D.
D.
 是抛物线
是抛物线
 上一点,经过点
上一点,经过点 的直线
的直线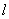 与抛物
与抛物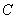 交于
交于 两点.
两点. (I)求证:
(I)求证: 为定值;
为定值; 的面积为
的面积为 ,求直线
,求直线 ,己知
,己知 ,且满足
,且满足 ,则该医院30天内因患H1N1流感就诊的人数共有 .
,则该医院30天内因患H1N1流感就诊的人数共有 .