题目内容
如果f(
)=
,则当x≠0且x≠1时,f(x)= .
| 1 |
| x |
| x |
| 1-x |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:利用换元法令
=t,则x=
,代入函数的表达式求出即可.
| 1 |
| x |
| 1 |
| t |
解答:
解:∵x≠0且x≠1,令
=t,则x=
,
∴f(t)=
=
,
∴f(x)=
,
故答案为:
.
| 1 |
| x |
| 1 |
| t |
∴f(t)=
| ||
1-
|
| 1 |
| t-1 |
∴f(x)=
| 1 |
| x-1 |
故答案为:
| 1 |
| x-1 |
点评:本题考查了求函数的解析式问题,换元法是常用方法之一,本题属于基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知f(x)为R上的可导函数,且?x∈R,均有f(x)>f′(x),则有( )
| A、e2014f(-2014)<f(0),f(2014)>e2014f(0) |
| B、e2014f(-2014)<f(0),f(2014)<e2014f(0) |
| C、e2014f(-2014)>f(0),f(2014)>e2014f(0) |
| D、e2014f(-2014)>f(0),f(2014)<e2014f(0) |
下列函数中,周期为π,且在[
,
]上为增函数的是( )
| π |
| 4 |
| π |
| 2 |
A、y=sin(x+
| ||
B、y=cos(x-
| ||
| C、y=-sin(2x-π) | ||
| D、y=cos(2x+π) |
函数f(x)=sinxcosx是( )
| A、最小正周期为2π且在[0,π]内有且只有三个零点的函数 |
| B、最小正周期为2π且在[0,π]内有且只有二个零点的函数 |
| C、最小正周期为π且在[0,π]内有且只有三个零点的函数 |
| D、最小正周期为π且在[0,π]内有且只有二个零点的函数 |
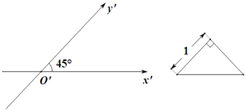 已知一个三棱锥的高为3,其底面用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如右图所示),则此三棱锥的体积为( )
已知一个三棱锥的高为3,其底面用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如右图所示),则此三棱锥的体积为( )