题目内容
已知α、β均为锐角,且sinα=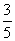 ,tan(α-β)=-
,tan(α-β)=- .
.
(1) 求sin(α-β)的值;
(2) 求cosβ的值.
解:(1) ∵ α、β∈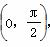 ,∴ -
,∴ - <α-β<
<α-β< .又tan(α-β)=-
.又tan(α-β)=- <0,∴ -
<0,∴ - <α-β<0.
<α-β<0.
∴ sin(α-β)=- .
.
(2) 由(1)可得,cos(α-β)= .
.
∵ α为锐角,sinα=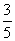 ,∴ cosα=
,∴ cosα=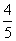 .
.
∴ cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)
=

练习册系列答案
相关题目
 ,α∈
,α∈ ,则sin2α=__________.
,则sin2α=__________. tan20°tan40°.
tan20°tan40°. =
= ,则sinθ+cosθ=________.
,则sinθ+cosθ=________.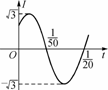
 ,则sinα=________.
,则sinα=________.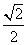 的直线l与椭圆
的直线l与椭圆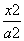 +
+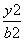 =1(a>b>0)有两个不同的交点,且这两个交点在x轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为________.
=1(a>b>0)有两个不同的交点,且这两个交点在x轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为________.