题目内容
4.设函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x+4,x<k}\\{4x+3,x≥k}\end{array}\right.$是(-∞,+∞)上的增函数,那么实数k的取值范围为(-∞,-1]∪[1,2].分析 根据函数的解析式、一元二次函数的单调性、函数单调性的性质,列出不等式组,求出实数k的取值范围.
解答 解:∵f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x+4,x<k}\\{4x+3,x≥k}\end{array}\right.$是(-∞,+∞)上的增函数,
∴$\left\{\begin{array}{l}{k≤2}\\{{-k}^{2}+4k+4≤4k+3}\end{array}\right.$,解得k≤-1或1≤k≤2,
则实数k的取值范围是(-∞,-1]∪[1,2],
故答案为:(-∞,-1]∪[1,2].
点评 本题考查函数单调性的性质,以及一元二次函数的单调性,注意端点处函数的大小关系.

练习册系列答案
相关题目
12.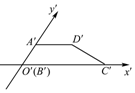 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )
 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{3}$ |
19.“a3>b3”是“a>b”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
9.“0<a<1”是“a<$\sqrt{a}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 中,
中, 的对边分别为
的对边分别为 ,且
,且

 的大小
的大小 求
求 的值
的值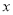 人,瓦工
人,瓦工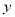 人,则工人满足的关系式是( )
人,则工人满足的关系式是( )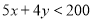 B.
B.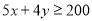
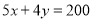 D.
D.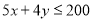
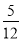 B.
B. C.
C. D.
D.