题目内容
18．抛掷一枚硬币，记$X=\left\{\begin{array}{l}1，{\;}^{\;}正面向上\\-1，反面向上\end{array}\right.$，则E（X）=（ ）| A． | 0 | B． | $\frac{1}{2}$ | C． | 1 | D． | -1 |
分析 由题意P（X=1）=$\frac{1}{2}$，P（X=-1）=$\frac{1}{2}$，由此能求出E（X）．
解答 解：∵抛掷一枚硬币，记$X=\left\{\begin{array}{l}1，{\;}^{\;}正面向上\\-1，反面向上\end{array}\right.$，
P（X=1）=$\frac{1}{2}$，P（X=-1）=$\frac{1}{2}$，
∴E（X）=1×$\frac{1}{2}+（-1）×\frac{1}{2}$=0．
故选：A．
点评 本题考查离散型随机变量的数学期望的求法，是基础题，解题时要认真审题，注意数学期望的性质的合理运用．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
8．过M（1，3）引圆x2+y2=2的切线，切点分别为A、B，则△AMB的面积为（ ）
| A． | $\frac{32}{5}$ | B． | 4 | C． | $\frac{16}{5}$ | D． | $\frac{8}{5}$ |
6．
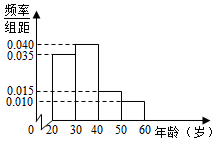某学校有120名教师，且年龄都在20岁到60岁之间，各年龄段人数按分组，其频率分布直方图如图所示，学校要求每名教师都要参加两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表示，假设两项培训是相互独立的，结业考试成绩也互不影响．
（1）若用分层抽样法从全校教师中抽取一个容量为40的样本，求从年龄段[20，30）抽取的人数；
（2）求全校教师的平均年龄；
（3）随机从年龄段[20，30）和[30，40）内各抽取1人，设这两人中两项培训结业考试成绩都优秀的人数为X，求X的概率分布和数学期望．
某学校有120名教师，且年龄都在20岁到60岁之间，各年龄段人数按分组，其频率分布直方图如图所示，学校要求每名教师都要参加两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表示，假设两项培训是相互独立的，结业考试成绩也互不影响．| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20，30） | 30 | 18 |
| [30，40） | 36 | 24 |
| [40，50） | 12 | 9 |
| [50，60] | 4 | 3 |
（2）求全校教师的平均年龄；
（3）随机从年龄段[20，30）和[30，40）内各抽取1人，设这两人中两项培训结业考试成绩都优秀的人数为X，求X的概率分布和数学期望．
已知F1（-$\sqrt{3}$，0），F2（$\sqrt{3}$，0）为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，点P在椭圆C上，且△PF1F2面积的最大值为$\sqrt{3}$．