Question

如图，四棱锥P-ABCD，侧面PAD是边长为2的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的棱形，M为棱PC上的动点，且

PM

PC

=λ（λ∈[0，1]）．
（1）求证：△PBC为直角三角形；
（2）试确定λ的值，使得二面角P-AD-M的平面角余弦值为

2 5

5

．

Answer 1

考点：二面角的平面角及求法,棱锥的结构特征

专题：空间位置关系与距离,空间角

分析：（1）取AD中点O，连结OP，OC，以O为原点，OC为x轴，OD为y轴，OP为z轴，建立空间直角坐标系，利用向量法能证明△PBC为直角三角形．
（2）设M（a，b，c），由

PM

PC

=λ（λ∈[0，1]），得M（

3

λ，0，

3

-

3

λ），求出平面AMD的法向量和平面PAD的法向量，由此利用向量法能求出结果．

解答： （1）证明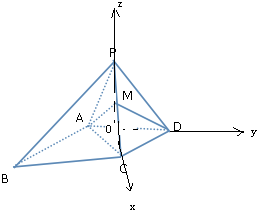：取AD中点O，连结OP，OC，
∵侧面PAD是边长为2的正三角形，且与底面垂直，
底面ABCD是∠ABC=60°的棱形，
∴△ADC是等边三角形，PO、AD、CO两两垂直，
以O为原点，OC为x轴，OD为y轴，OP为z轴，
建立空间直角坐标系，
由题意得P（0，0，

3

），C（

3

，0，0），
B（

3

，-2，0），

CB

=（0，-2，0），

CP

=（-

3

，0，

3

），
∴

CB

•

CP

=0，∴CB⊥CP，
∴△PBC为直角三角形．
（2）解：设M（a，b，c），∵

PM

PC

=λ（λ∈[0，1]），
∴

PM

=λ

PC

，即（a，b，c-

3

）=（

3

λ，0，-

3

λ），∴M（

3

λ，0，

3

-

3

λ），
A（0，-1，0），D（0，1，0），

AD

=（0，2，0），

AM

=（

3

λ，1，

3

-

3

λ），
设平面AMD的法向量

n

=（x，y，z），
则

n • AD =2y=0 n • AM = 3 λx+y+( 3 - 3 λ)z=0

，
取x=1，得

n

=（1，0，

λ-1

λ

），
由题意平面PAD的法向量

m

=（1，0，0），
∵二面角P-AD-M的平面角余弦值为

2 5

5

．
∴|cos＜

m

，

n

＞|=|

1

1+( λ-1 λ )2

|=

2 5

5

，
由λ∈[0，1]），解得λ=

1

3

．

点评：本题考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．