题目内容
 如图,在直角坐标系xOy中,已知圆O:x2+y2=4,点A(1,0),B为直线x=4上任意一点,直线AB交圆O于不同两点M,N.
如图,在直角坐标系xOy中,已知圆O:x2+y2=4,点A(1,0),B为直线x=4上任意一点,直线AB交圆O于不同两点M,N.(1)若MN=
| 14 |
(2)若
| MA |
| AN |
(3)设
| AM |
| MB |
| AN |
| NB |
分析:(1)设AB的方程y=k(x-1),利用垂径定理和点到直线的距离公式,结合题意建立关于k的等式解出k=±1,可得直线AB的方程,进而算出点B的坐标;
(2)设M(x1,y1)N(x2,y2),根据由
=2
求出用x2、y2表示x1、y1的式子,代入圆方程化简得到N点的坐标,利用直线的斜率公式算出AB的斜率,可得直线AB的方程;
(3)由
=λ
、
=μ
,利用向量的坐标运算法则算出λ=
、μ=
.由直线AB方程与圆方程消去y得到关于x的一元二次方程,利用根与系数的关系化简λ+μ关于x1+x2、x1x2的式子,可得λ+μ=0(定值).
(2)设M(x1,y1)N(x2,y2),根据由
| MA |
| AN |
(3)由
| AM |
| MB |
| AN |
| NB |
| x1-1 |
| 4-x1 |
| x2-1 |
| 4-x2 |
解答:解:(1)设直线AB的方程y=k(x-1),即kx-y-k=0
∵MN=
,∴根据垂径定理,得
=2
,解之得d=
,
由点到直线的距离公式,得
=
,解之得k=±1,
∴直线AB的方程y=±(x-1),
结合B的横坐标为4,代入直线方程求得y=±3,得点B的坐标为B(4,±3).
(2)设M(x1,y1),N(x2,y2),
由
=2
,得
∴代入圆的方程,得
,解之得
,
∴直线AB的斜率为kAB=
=±
,可得直线AB的方程为y=±
(x-1).
(3)设M(x1,y1)N(x2,y2),
由
=λ
,得x1-1=λ(4-x1),解得λ=
,同理得到μ=
,
∴λ+μ=
由
消去y,得(1+k2)x2-2k2x+k2-4=0
∴
,可得λ+μ=
=0,即λ+μ=0(定值).
∵MN=
| 14 |
| 14 |
| 22-d2 |
| ||
| 2 |
由点到直线的距离公式,得
| |k| | ||
|
| ||
| 2 |
∴直线AB的方程y=±(x-1),
结合B的横坐标为4,代入直线方程求得y=±3,得点B的坐标为B(4,±3).
(2)设M(x1,y1),N(x2,y2),
由
| MA |
| AN |
|
∴代入圆的方程,得
|
|
∴直线AB的斜率为kAB=
±
| ||||
|
| ||
| 3 |
| ||
| 3 |
(3)设M(x1,y1)N(x2,y2),
由
| AM |
| MB |
| x1-1 |
| 4-x1 |
| x2-1 |
| 4-x2 |
∴λ+μ=
| 5(x1+x 2)-2x1x2-8 |
| 16-4(x1+x2) |
由
|
∴
|
5•
| ||||
16-4•
|
点评:本题着重考查了向量的坐标运算、直线的基本量与基本形式、直线与圆的位置关系和一元二次方程根与系数的关系等知识,属于中档题.

练习册系列答案
相关题目
 (2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.
(2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.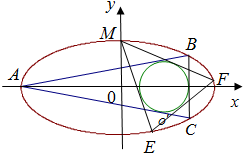 如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为 (2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
(2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且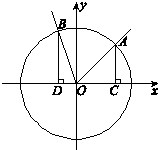 如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: