题目内容
11. 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中,(1)求证直线BD与平面A1B1C1D1平行;
(2)求证:面BB1DD1⊥面AB1C
(3)求二面角A-B1C-C1的大小.
分析 (1)由BD∥B1D1,能证明直线BD与平面A1B1C1D1平行.
(2)推导出D1D⊥AC,AC⊥BD,从而AC⊥面DD1B1B,由此能证明面BB1DD1⊥面AB1C.
(3)取B1C的中点E,连接AE,EC1.推导出∠AEC1为二面角A-B1C-C1的平面角,由此能求出二面角A-B1C-C1的大小.
解答 证明:(1)∵正方体ABCD-A1B1C1D1中,BD∥B1D1,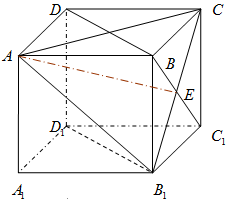
BD?平面A1B1C1D1,B1D1?平面A1B1C1D1,
∴直线BD与平面A1B1C1D1平行.
(2)∵D1D⊥面ABCD,AC?面ABCD,
∴D1D⊥AC,
又∵在正方形ABCD中,∴由正方形性质得AC⊥BD,
∵D1D∩BD=D,∴AC⊥面DD1B1B,
又∵AC?面AB1C,∴面BB1DD1⊥面AB1C.
(3)如图,取B1C的中点E,连接AE,EC1.
∵AC,AB1,B1C分别为正方形的对角线,∴AC=AB1=B1C,
∵E是B1C的中点∴AE⊥B1C,
又∵在正方形BB1C1C中,∴由正方形性质得EC1⊥B1C,
∴∠AEC1为二面角A-B1C-C1的平面角,
设正方体ABCD-A1B1C1D1中棱长为2,
则AB1=AC=B1C=$\sqrt{4+4}=2\sqrt{2}$,AE=$\sqrt{8-2}$=$\sqrt{6}$,
C1E=$\sqrt{2}$,AC1=$\sqrt{4+4+4}$=2$\sqrt{3}$,
∴cos∠AEC1=$\frac{A{E}^{2}+E{{C}_{1}}^{2}-A{{C}_{1}}^{2}}{2AE•E{C}_{1}}$=$\frac{6+2-12}{2•\sqrt{6}•\sqrt{2}}$=-$\frac{\sqrt{3}}{3}$,
∴∠AEC1=$π-arccos\frac{\sqrt{3}}{3}$.
∴二面角A-B1C-C1的大小为$π-arccos\frac{\sqrt{3}}{3}$.
点评 本题考查线面平行的证明,考查面面垂直的证明,考查二面角的求法,考查空间想象能力与计算能力,考查等价转化思想、数形结合思想,是中档题.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案| A. | a>b>d>c | B. | b>a>d>c | C. | a>c>b>d | D. | c>a>b>d |
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
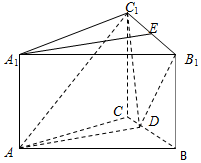 如图,在正三棱柱ABC-A1B1C1中,点D为为边BC的中点,AB=4,AA1=2.
如图,在正三棱柱ABC-A1B1C1中,点D为为边BC的中点,AB=4,AA1=2.