题目内容
9.点P是双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$上的点,F1,F2分别是双曲线的左右焦点,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,则|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|=( )| A. | 48 | B. | 32 | C. | 16 | D. | 24 |
分析 根据双曲线的方程得到a,c的值,设|$\overrightarrow{P{F}_{1}}$|=m,|$\overrightarrow{P{F}_{2}}$|=n,根据双曲线的定义可得n-m=4,再根据垂直和勾股定理可得答案
解答 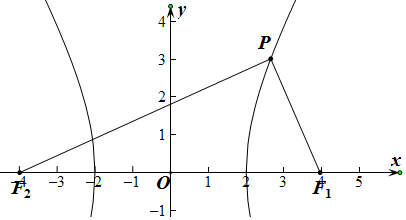 解:设|$\overrightarrow{P{F}_{1}}$|=m,|$\overrightarrow{P{F}_{2}}$|=n,
解:设|$\overrightarrow{P{F}_{1}}$|=m,|$\overrightarrow{P{F}_{2}}$|=n,
∵a=2,c=4,
∴n-m=2a=4,
∴(n-m)2=16,
即n2+m2-2mn=16
∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,
∴$\overrightarrow{P{F}_{1}}$⊥$\overrightarrow{P{F}_{2}}$,
∴n2+m2=4c2=64,
∴64-2mn=16,
∴mn=24,
即|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|=24,
故选:D
点评 本题考查了双曲线的简单性质,以及向量的数量积和向量的垂直的关系,属于基础题.

练习册系列答案
相关题目
12. 已知程序框图如图,则输出的i的值是( )
已知程序框图如图,则输出的i的值是( )
 已知程序框图如图,则输出的i的值是( )
已知程序框图如图,则输出的i的值是( )| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
9.设函数f(0)x=sinx,定义f(1)x=f′[f(0)(x)],f(2)(x)=f′[f(1)(x)],…,f(n)(x)=f′[f(n-1)(x)],则f(1)(150)+f(2)(150)+f(3)(150)+…+f(2017)(150)的值是( )
| A. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | 0 | D. | 1 |
4.定义在R上的函数f(x)满足f(x)+f′(x)>2,ef(1)=2e+4,则不等式f(x)>$\frac{4}{{e}^{x}}$+2(其中e为自然对数的底数)的解集为( )
| A. | (1,+∞) | B. | (-∞,0)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,1) |
1.在△ABC中,∠BAC=90°,AD是BC边上的高,则相似三角形共有( )
| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
18.设某校新、老校区之间开车单程所需时间为T,T只与道路畅通状况有关,对其容量为200的样本进行统计,结果如下:
(1)求T的分布列与数学期望ET;
(2)唐教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求唐教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
| T(分钟) | 25 | 30 | 35 | 40 |
| 频数(次) | 40 | 60 | 80 | 20 |
(2)唐教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求唐教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中,