题目内容
已知tanα，tanβ是方程7x2-8x+1=0的两根，则tan
的值为 ．
| α+β |
| 2 |
考点：半角的三角函数,两角和与差的正切函数
专题：计算题,三角函数的求值
分析：依题意，利用韦达定理可求得tanα+tanβ与tanαtanβ的值，再利用两角和的正切可求得tan（α+β），从而可知tan
的值
| α+β |
| 2 |
解答：
解：∵tanα、tanβ是方程7x2-8x+1=0的两根，
∴tanα+tanβ=
，tanαtanβ=
，
∴tan（α+β）=
=
，
设tan
=x，则tan（α+β）=
∴
=
，
∴x=-2或
．
故答案为：-2或
．
∴tanα+tanβ=
| 8 |
| 7 |
| 1 |
| 7 |
∴tan（α+β）=
| tanα+tanβ |
| 1-tanαtanβ |
| 4 |
| 3 |
设tan
| α+β |
| 2 |
| 2x |
| 1-x2 |
∴
| 2x |
| 1-x2 |
| 4 |
| 3 |
∴x=-2或
| 1 |
| 2 |
故答案为：-2或
| 1 |
| 2 |
点评：本题考查两角和与差的正切函数，考查韦达定理的应用，属于中档题．
练习册系列答案
相关题目
函数f（x）=log0.2（x2-2x+2）的单调递减区间是（ ）
| A、[1，+∞） |
| B、[1，2] |
| C、[1，2） |
| D、[2，+∞） |
已知命题p：?x0∈R，sinx0≥
，则￢p是（ ）
| 1 |
| 2 |
A、?x0∈R，sinx0≤
| ||
B、?x0∈R，sinx0＜
| ||
C、?x∈R，sinx≤
| ||
D、?x∈R，sinx＜
|
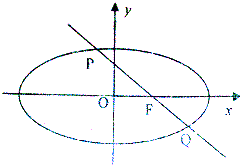已知椭圆的中心在原点，右焦点为F（3，0）过焦点F的直线l交P，Q两点线段PQ的中点为M（2，1）．求：