题目内容
11.已知?(x)=sin (x+$\frac{π}{6}$),若cos α=$\frac{3}{5}$(0<α<$\frac{π}{2}$),则f(α+$\frac{π}{12}$)=$\frac{7\sqrt{2}}{10}$.分析 由cos α=$\frac{3}{5}$(0<α<$\frac{π}{2}$),得sinα=$\frac{4}{5}$,则f(α+$\frac{π}{12}$)=sin(α+$\frac{π}{4}$)=sinαcos$\frac{π}{4}$+cosαsin$\frac{π}{4}$即可
解答 解:∵cos α=$\frac{3}{5}$(0<α<$\frac{π}{2}$),∴sinα=$\frac{4}{5}$
f(α+$\frac{π}{12}$)=sin(α+$\frac{π}{4}$)=sinαcos$\frac{π}{4}$+cosαsin$\frac{π}{4}$=$\frac{4}{5}×\frac{\sqrt{2}}{2}+\frac{3}{5}×\frac{\sqrt{2}}{2}=\frac{7\sqrt{2}}{10}$
故答案为:$\frac{7\sqrt{2}}{10}$
点评 本题考查了三角函数的求值,考查了三角公式的应用,属于中档题,

练习册系列答案
相关题目
2.若函数f(x)在R上可导,且满足f(x)<x f′(x),则( )
| A. | 2 f(1)<f(2) | B. | 2 f(1)>f(2) | C. | 2 f(1)=f(2) | D. | f(1)=f(2) |
19.已知不等式(m2+4m-5)x2-4(m-1)x+3>0对一切实数x恒成立,则实数m的取值范围为( )
| A. | (-∞,-5)∪(1,+∞) | B. | (1,19) | C. | [1,19) | D. | (19,+∞) |
1.下列说法正确的是( )
| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| C. | a∈R,“$\frac{1}{a}$<1”是“a>1”的必要不充分条件 | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题 |
 ,那么
,那么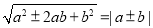 ,那么如何将双重二次根式
,那么如何将双重二次根式
 化简呢?如能找到两个数
化简呢?如能找到两个数
 ,使得
,使得 即
即 ,且使
,且使 即
即 ,那么
,那么
 ,双重二次根式得以化简;例如化简:
,双重二次根式得以化简;例如化简: ;
;  且
且 ,
,
 由此对于任意一个二次根式只要可以将其化成
由此对于任意一个二次根式只要可以将其化成 使得
使得 ,且
,且 ,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题: _________________;
_________________; __________________;
__________________; ②
② (每题2分)
(每题2分)