题目内容
变量 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
A
解析试题分析:确定不等式表示的区域,化简目标函数,利用图象即可求得结论.解:不等式表示的区域如图所示,
三个交点坐标分别为(0,1),( ,3),(2,0)目标函数z=3|x|+|y-3|=3x-y+3,即y=-3x+z-3,∴目标函数过(2,0)时,取得最大值为9,过(
,3),(2,0)目标函数z=3|x|+|y-3|=3x-y+3,即y=-3x+z-3,∴目标函数过(2,0)时,取得最大值为9,过( ,3)时,取得最小值为
,3)时,取得最小值为 ∴目标函数z=3|x|+|y-3|的取值范围是
∴目标函数z=3|x|+|y-3|的取值范围是 故选A.
故选A.
考点:线性规划
点评:本题考查线性规划知识的运用,考查数形结合的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
设动点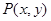 满足
满足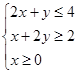 ,则
,则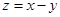 的最小值是( )
的最小值是( )
| A.2 | B.-4 | C.-1 | D.4 |
设不等式组  所表示的平面区域是
所表示的平面区域是 ,平面区域
,平面区域 与
与 关于直线
关于直线 对称.对于
对称.对于 中的任意一点
中的任意一点 与
与 中的任意一点
中的任意一点 ,
, 的最小值等于( )
的最小值等于( )
A. | B.4 | C. | D.2 |
设x,y满足约束条件 ,若目标函数
,若目标函数 的最小值为2,则
的最小值为2,则 的最大值是
的最大值是
| A.1 | B. | C. | D. |
设变量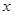 ,
,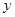 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最小值为
的最小值为
A. | B. | C. | D. |
若变量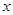 、
、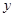 满足约束条件
满足约束条件 则目标函数
则目标函数 的最小值。( )
的最小值。( )
A. | B. | C. | D. |
如果实数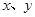 满足条件
满足条件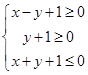 ,那么
,那么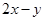 的最大值为( )
的最大值为( )
A.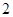 | B.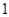 | C. | D.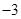 |
设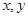 满足约束条件
满足约束条件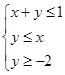 ,则
,则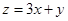 的最大值为 ( )
的最大值为 ( )
| A.5 | B.3 | C.7 | D.-8 |
设实数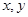 满足约束条件:
满足约束条件: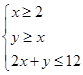 ,则
,则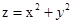 的最大值为( )。
的最大值为( )。
A.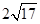 | B.68 | C.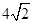 | D.32 |