题目内容
8.已知向量$\overrightarrow{a}$=(2sin$\frac{x}{4}$,2sin$\frac{x}{4}$),$\overrightarrow{b}$=(cos$\frac{x}{4}$,-$\sqrt{3}$sin$\frac{x}{4}$).(Ⅰ)求函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$+$\sqrt{3}$的最小正周期;
(Ⅱ)若β=$\frac{2sinα}{f(2α+\frac{π}{3})}$,g(β)=tan2α,α≠$\frac{π}{4}$+$\frac{kπ}{2}$且α≠$\frac{π}{2}$+kπ(k∈Z),数列{an}满足a1=$\frac{1}{4}$,an+12=$\frac{1}{2}$ang(an)(n≤16且n∈N*),令bn=$\frac{1}{{{a}_{n}}^{2}}$,求数列{bn}的通项公式及前n项和Sn.
分析 (I)利用数量积运算性质、倍角公式与和差公式可得:f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$+$\sqrt{3}$=$2sin(\frac{x}{2}+\frac{π}{3})$.即可得出f(x)的最小正周期为T=4π.
(II)$f(2α+\frac{π}{3})$=$2sin(α+\frac{π}{2})$=2cosα,可得β=$\frac{2sinα}{f(2α+\frac{π}{3})}$=tanα,g(β)=tan2α=$\frac{2β}{1-{β}^{2}}$,α≠$\frac{π}{4}$+$\frac{kπ}{2}$且α≠$\frac{π}{2}$+kπ(k∈Z),由数列{an}满足a1=$\frac{1}{4}$,an+12=$\frac{1}{2}$ang(an)(n≤16且n∈N*),可得an+12=$\frac{1}{2}$an×$\frac{2{a}_{n}}{1-{a}_{n}^{2}}$=$\frac{{a}_{n}^{2}}{1-{a}_{n}^{2}}$,取倒数可得:$\frac{1}{{a}_{n+1}^{2}}$-$\frac{1}{{a}_{n}^{2}}$=-1,即bn+1-bn=-1.b1=16.再利用等差数列的通项公式与求和公式即可得出.
解答 解:(I)f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$+$\sqrt{3}$=2sin$\frac{x}{4}$•cos$\frac{x}{4}$+2$sin\frac{x}{4}$×(-$\sqrt{3}$sin$\frac{x}{4}$)+$\sqrt{3}$=$sin\frac{x}{2}$+$\sqrt{3}$$cos\frac{x}{2}$=$2sin(\frac{x}{2}+\frac{π}{3})$.
∴f(x)的最小正周期为T=$\frac{2π}{\frac{1}{2}}$=4π.
(II)$f(2α+\frac{π}{3})$=$2sin(α+\frac{π}{2})$=2cosα,∴β=$\frac{2sinα}{f(2α+\frac{π}{3})}$=$\frac{2sinα}{2cosα}$=tanα,
g(β)=tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{2β}{1-{β}^{2}}$,α≠$\frac{π}{4}$+$\frac{kπ}{2}$且α≠$\frac{π}{2}$+kπ(k∈Z),
∵数列{an}满足a1=$\frac{1}{4}$,an+12=$\frac{1}{2}$ang(an)(n≤16且n∈N*),
∴an+12=$\frac{1}{2}$an×$\frac{2{a}_{n}}{1-{a}_{n}^{2}}$=$\frac{{a}_{n}^{2}}{1-{a}_{n}^{2}}$,取倒数可得:$\frac{1}{{a}_{n+1}^{2}}$-$\frac{1}{{a}_{n}^{2}}$=-1,即bn+1-bn=-1.b1=16.
∴数列{bn}的通项公式bn=16-(n-1)=17-n,(n≤16且n∈N*),
前n项和Sn=$\frac{(16+17-n)}{2}×n$=$\frac{33n-{n}^{2}}{2}$,(n≤16且n∈N*).
点评 本题考查了数量积运算性质、倍角公式与和差公式、数列递推关系、等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于难题.

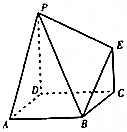 如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,则二面角A-PB-E的大小为( )
如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,则二面角A-PB-E的大小为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{8}$ |
| A. | x=1 | B. | x=$\frac{1}{2}$ | C. | x=-1 | D. | x=-$\frac{1}{2}$ |
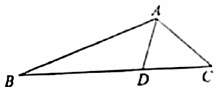 如图,已知AD是△ABC内角∠BAC的角平分线.
如图,已知AD是△ABC内角∠BAC的角平分线.