题目内容
13．在△ABC中，已知sinA：sinB：sinC=3：5：7，则此三角形的最大内角为（ ）| A． | 75° | B． | 120° | C． | 135° | D． | 150° |
分析 由题意和正弦定理得a：b：c=3：5：7，不妨设a=3k，b=5k，c=7k，（k＞0），由边角关系可得C是最大角，利用余弦定理求出cosB的值，由内角的范围和特殊角的三角函数值求出B．
解答 解：因为sinA：sinB：sinC=3：5：7，
所以由正弦定理得a：b：c=3：5：7，
不妨设a=3k，b=5k，c=7k，（k＞0），
则角C是最大角，由余弦定理得，
cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{9{k}^{2}+25{k}^{2}-49{k}^{2}}{2×3k×5k}$=$-\frac{1}{2}$，
因为0°＜C＜180°，所以C=120°，
故选B．
点评 本题考查了正弦定理和余弦定理的综合应用，以及边角关系，考查化简、计算能力．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
3．若（$\root{n}{-3}$）n有意义，则n一定是（ ）
| A． | 正偶数 | B． | 正整数 | C． | 正奇数 | D． | 整数 |
8．在△ABC中，若c=2acosB，则△ABC的形状一定是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | ||
| C． | 等腰或直角三角形 | D． | 等腰三角形 |
18．下列函数中，既不是奇函数，也不是偶函数的是（ ）
| A． | y=x+sin 2x | B． | y=x2-cos x | C． | y=2x+$\frac{1}{{2}^{x}}$ | D． | y=x2+sin x |
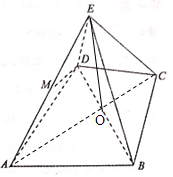如图几何体E-ABCD是四棱锥，△ABD为正三角形，∠BCD=120°，CB=CD=CE=1，AB=AD=AE=$\sqrt{3}$，且EC⊥BD，