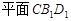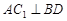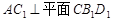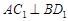题目内容
如图,在四棱台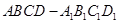 中,底面
中,底面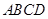 是平行四边形,
是平行四边形,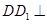 平面
平面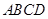 ,
, ,
, ,
,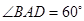 .
.
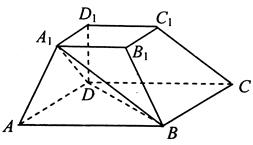
(1)证明: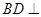 平面
平面 ;
;
(2)证明: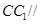 平面
平面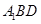 .
.
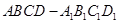 中,底面
中,底面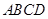 是平行四边形,
是平行四边形,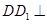 平面
平面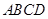 ,
, ,
, ,
,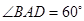 .
.
(1)证明:
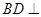 平面
平面 ;
;(2)证明:
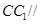 平面
平面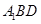 .
.(1)详见解析;(2)详见解析.
试题分析:(1)先用余弦定理确定
 与
与 的等量关系,利用勾股定理得到
的等量关系,利用勾股定理得到 ,再用
,再用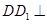 平面
平面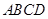 得到
得到 ,最后利用直线与平面垂直的判定定理得到
,最后利用直线与平面垂直的判定定理得到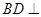 平面
平面 ;(2)连接
;(2)连接 、
、 ,设
,设 ,连接
,连接 ,利用棱台底面的相似比得到
,利用棱台底面的相似比得到 ,从而证明四边形
,从而证明四边形 为平行四边形,得到
为平行四边形,得到 ,最后利用直线与平面平行的判定定理得到
,最后利用直线与平面平行的判定定理得到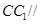 平面
平面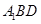 .
.试题解析:(1)
 ,
,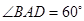 ,在
,在 中,由余弦定理得
中,由余弦定理得 ,
,
 ,因此,
,因此,
 平面
平面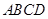 ,且
,且 平面
平面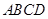 ,
, ,
,又
 ,
, 平面
平面 ;
;(2)连接
 、
、 ,设
,设 ,连接
,连接 ,
, 四边形
四边形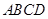 是平行四边形,
是平行四边形, ,
,
由棱台定义及
 知
知 ,且
,且 ,
, 四边形
四边形 是平行四边形,因此
是平行四边形,因此
又
 平面
平面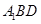 ,
, 平面
平面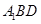 ,
, 平面
平面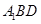 .
.
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
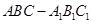 中,
中,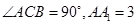 ,
,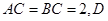 为
为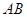 中点,
中点,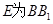 上一点,且
上一点,且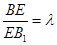 .
.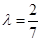 时,求证:
时,求证: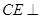 平面
平面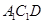 ;
; 与平面
与平面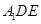 所成的角为
所成的角为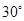 ,求
,求 的值.
的值.
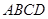 中,
中,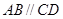 ,
,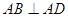 ,且
,且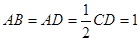 .
.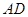 为一边向梯形外作正方形
为一边向梯形外作正方形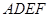 ,然后沿边
,然后沿边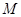 为
为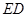 的中点,如图2.
的中点,如图2.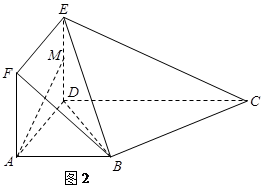
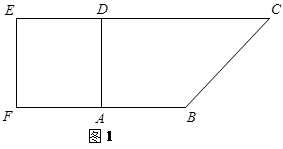
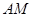 ∥平面
∥平面 ;
;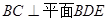 ;
; 到平面
到平面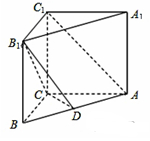
 中,
中,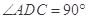 ,
,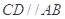 ,
,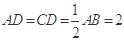 ,点
,点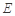 为
为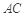 中点.将
中点.将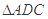 沿
沿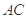 折起,使平面
折起,使平面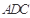
 平面
平面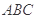 ,得到几何体
,得到几何体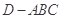 ,如图2所示.
,如图2所示.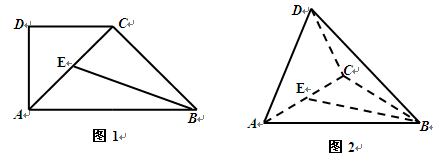
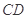 上找一点
上找一点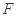 ,使
,使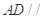 平面
平面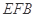 ;
;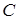 到平面
到平面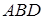 的距离.
的距离.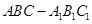 的底面边长是
的底面边长是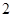 ,侧棱长是
,侧棱长是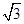 ,
,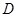 是
是 的中点.
的中点.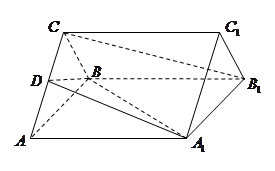
 ∥平面
∥平面 ;
;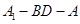 的大小;
的大小;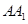 上是否存在一点
上是否存在一点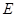 ,使得平面
,使得平面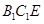
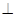 平面
平面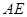 的长;若不存在,说明理由.
的长;若不存在,说明理由.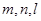 和两个不重合的平面
和两个不重合的平面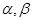 ,下列命题正确的是( )
,下列命题正确的是( )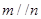 ,
,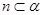 ,则
,则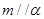
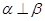 ,
,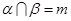 ,且
,且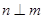 ,则
,则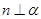
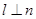 ,
,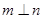 ,则
,则
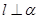 ,
,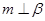 ,且
,且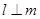 ,则
,则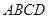 -
-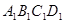 为正方体,下列结论错误的是( )
为正方体,下列结论错误的是( )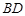 ∥
∥