题目内容
正方体ABCD-A1B1C1D1的对角线AC1的长为3cm,则它的体积为( )
| A、4cm3 | ||
| B、8cm3 | ||
C、
| ||
D、3
|
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:利用正方体对角线长度计算公式求棱长,再求正方体的体积.
解答:
解:∵正方体ABCD-A1B1C1D1的对角线AC1的长为3cm,
∴正方体的棱长为
cm,
∴体积为3
cm3.
故选:D.
∴正方体的棱长为
| 3 |
∴体积为3
| 3 |
故选:D.
点评:本题考查了正方体的对角线计算公式,考查正方体的体积,比较基础.

练习册系列答案
相关题目
下表是某厂1到4月份用水量情况(单位:百吨)的一组数据:
用水量y与月份x之间具有线性相关关系,其线性回归方程为
=-0.7x+a,则a的值为( )
| 月份x | 1 | 2 | 3 | 4 |
| 用水量ym3 | 4.5 | 4 | 3 | 2.5 |
| ∧ |
| y |
| A、5.25 | B、5 |
| C、2.5 | D、3.5 |
某学校高一年级有35个班,每个班有56名同学都是从1到56编的号码.为了交流学习经验,要求每班号码为14的同学留下进行交流,这里运用的是( )
| A、分层抽样 | B、抽签抽样 |
| C、随机抽样 | D、系统抽样 |
定义方程f(x)=f′(x)的实数根x0叫做f(x)的“新驻点”,若函数g(x)=x;h(x)=lnx;φ(x)=x3+1(0<x<2)的“新驻点”分别为α,β,γ,则( )
| A、β<α<γ |
| B、γ<β<α |
| C、γ<α<β |
| D、α<γ<β |
设向量
=(cos23°,cos97°),
=(sin97°,sin23°),则
•
等于( )
| a |
| b |
| a |
| b |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
已知函数f(x)=
,则满足f(x)≤2的x的取值范围是( )
|
| A、[-1,2] |
| B、[0,2] |
| C、[1,+∞) |
| D、[-1,+∞) |
已知函数f(x)=
,则f(lg2+lg5)=( )
|
| A、10 | B、1 | C、0 | D、-1 |
已知向量
、
,
•
=-40,|
|=10,|
|=8,则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、60° | B、-60° |
| C、120° | D、-120° |
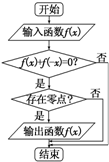 某流程图如图所示,现输入如下四个函数
某流程图如图所示,现输入如下四个函数