题目内容
19.在三角形ABC中,有三边a,b,c,已知$\frac{1+cosB}{sinA}$=$\frac{\sqrt{3}b}{a}$,求∠B为多少?分析 利用正弦定理将边化角,化简即可得出sinB,cosB的关系,利用同角三角函数的关系求出cosB,得出B的值.
解答 解:在三角形ABC中,∵$\frac{1+cosB}{sinA}$=$\frac{\sqrt{3}b}{a}$=$\frac{\sqrt{3}sinB}{sinA}$,
∴1+cosB=$\sqrt{3}$sinB,即cosB=$\sqrt{3}$sinB-1.
∵sin2B+cos2B=1,
∴4sin2B-2$\sqrt{3}$sinB=0,解得sinB=$\frac{\sqrt{3}}{2}$或sinB=0(舍),
∴cosB=$\sqrt{3}×\frac{\sqrt{3}}{2}-1$=$\frac{1}{2}$.
∴B=$\frac{π}{6}$.
点评 本题考查了正弦定理,同角三角函数的关系,属于中档题.

练习册系列答案
相关题目
14.抛物线y2=8x的焦点为F,其准线与x轴的交点为Q,过点F作直线与此抛物线交于A,B两点,若$\overrightarrow{FA}$•$\overrightarrow{QB}$=0,则|AF|-|BF|=( )
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
4.已知x,y满足线性约束条件$\left\{\begin{array}{l}x-2y≤0\\ x+y-4≤0\\ 2x+y-4≥0\end{array}$,则目标函数z=$\frac{x+1}{y+2}$的最小值为( )
| A. | $\frac{1}{6}$ | B. | $\frac{11}{10}$ | C. | $\frac{13}{14}$ | D. | $\frac{10}{11}$ |
8.已知点(a,1)到直线x-y+1=0的距离为1,则a的值为( )
| A. | 1 | B. | -1 | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
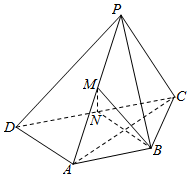 如图,在四棱锥P-ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点.
如图,在四棱锥P-ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点.
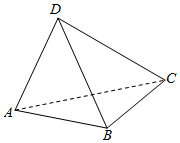 如图,在三棱锥D-ABC中,已知AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设AD=a,BC=b,CD=c,则$\frac{c^2}{ab+1}$的最小值为2.
如图,在三棱锥D-ABC中,已知AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设AD=a,BC=b,CD=c,则$\frac{c^2}{ab+1}$的最小值为2.