题目内容
已知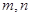 为异面直线,
为异面直线,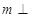 平面
平面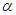 ,
,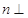 平面
平面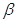 .直线
.直线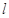 满足
满足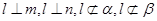 ,则( )
,则( )
A.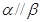 ,且 ,且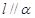 |
B.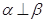 ,且 ,且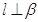 |
C.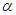 与 与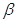 相交,且交线垂直于 相交,且交线垂直于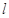 |
D.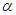 与 与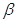 相交,且交线平行于 相交,且交线平行于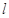 |
D
解析试题分析:因为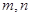 为异面直线,
为异面直线,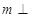 平面
平面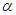 ,
,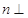 平面
平面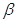 ,所以
,所以 与
与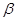 不平行是相交,则交线分别垂直于异面直线
不平行是相交,则交线分别垂直于异面直线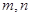 ;又直线
;又直线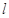 满足
满足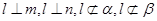 ,所以交线平行于
,所以交线平行于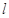 .
.
考点:点、线、面的位置关系.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
对于空间的两条直线 ,
, 和一个平面
和一个平面 ,下列命题中的真命题是( )
,下列命题中的真命题是( )
A.若 , , ,则 ,则 | B.若  , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , ,  ,则 ,则 |
设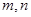 是空间两条直线,
是空间两条直线,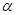 ,
, 是空间两个平面,则下列选项中不正确的是( )
是空间两个平面,则下列选项中不正确的是( )
A.当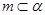 时,“ 时,“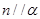 ”是“ ”是“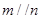 ”的必要不充分条件 ”的必要不充分条件 |
B.当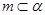 时,“ 时,“ ”是“ ”是“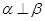 ”的充分不必要条件 ”的充分不必要条件 |
C.当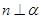 时, “ 时, “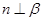 ”是“ ”是“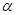 ∥ ∥ ”成立的充要条件 ”成立的充要条件 |
D.当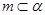 时,“ 时,“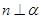 ”是“ ”是“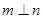 ”的充分不必要条件 ”的充分不必要条件 |
已知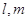 是两条不同的直线,
是两条不同的直线,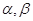 是两个不同的平面,在下列条件中,能成为
是两个不同的平面,在下列条件中,能成为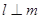 的充分条件的是( )
的充分条件的是( )
A.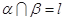 , ,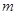 与 与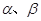 所成角相等 所成角相等 |
B.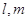 在 在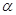 内的射影分别为 内的射影分别为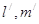 ,且 ,且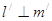 |
C.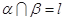 , ,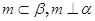 |
D.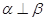 , ,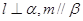 |
对于直线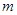 ,
,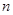 和平面
和平面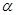 ,
,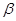 ,使
,使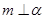 成立的一个充分条件是( )
成立的一个充分条件是( )
A.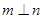 , ,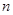 ∥ ∥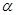 | B.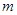 ∥ ∥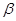 , ,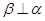 |
C.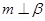 , ,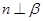 , , | D.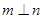 , ,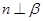 , ,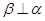 |
已知正四棱柱 中
中 为
为 的中点,则直线
的中点,则直线 与平面
与平面 的距离为( )
的距离为( )
A. | B. | C. | D. |
 ,下列说法正确的有: ___________.
,下列说法正确的有: ___________.
 点在线段
点在线段 上运动,棱锥
上运动,棱锥 体积不变;
体积不变; 所成角不变;
所成角不变; 截此正方体,如果截面是三角形,则必为锐角三角形;
截此正方体,如果截面是三角形,则必为锐角三角形; 与平面
与平面 间平行移动时此六边形周长先增大,后减小。
间平行移动时此六边形周长先增大,后减小。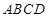 -
-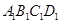 ,
,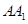 =2,
=2,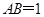 ,
,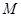 ,
,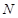 分别在
分别在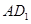 ,
,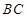 上移动,且始终保持
上移动,且始终保持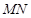 ∥平面
∥平面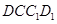 ,设
,设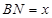 ,
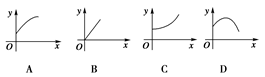
,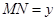 ,则函数
,则函数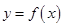 的图象大致是( )
的图象大致是( )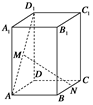
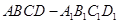 的棱长为1,
的棱长为1,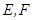 分别为线段
分别为线段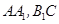 上的动点,则三棱锥
上的动点,则三棱锥 的体积为________.
的体积为________.