题目内容
15.在△ABC中,角A,B,C对应的边分别是a,b,c且cos2B+3cosB-1=0.(1)求角B的大小;
(2)若a+c=1,求b的最小值.
分析 (1)利用二倍角的余弦函数公式化简已知可得2cos2B+3cosB-2=0,解得cosB,从而可求B的值.
(2)由已知及余弦定理可得b2=3a2-3a+1,其中0<a<1,由于二次函数f(a)=3a2-3a+1在$(0,\frac{1}{2}]$上递减,在$[\frac{1}{2},1)$上递增,从而可求b2的最小值,进而得解b的最小值.
解答 解:(1)在△ABC中,∵cos2B+3cosB-1=0,
∴2cos2B+3cosB-2=0,
∴$cosB=\frac{1}{2}$或cosB=-2(舍去),
∴$B=\frac{π}{3}$.
(2)∵a+c=1,由余弦定理,得b2=a2+c2-2accosB=(a+c)2-3ac=1-3a(1-a)=3a2-3a+1,其中0<a<1,
∵f(a)=3a2-3a+1在$(0,\frac{1}{2}]$上递减,在$[\frac{1}{2},1)$上递增,
∴$b_{min}^2=f(\frac{1}{2})=\frac{1}{4}$,又0<b<1,
∴${b_{min}}=\frac{1}{2}$.
点评 本题主要考查了二倍角的余弦函数公式,余弦定理,二次函数的图象和性质在解三角形中的综合应用,考查了转化思想和数形结合思想的应用,考查了计算能力,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
4.下列函数中,与函数y=-x3的奇偶性、单调性相同的是( )
| A. | y=$\frac{1}{x}$ | B. | y=-tanx | C. | y=log${\;}_{\frac{1}{2}}$x | D. | y=$\frac{1}{{2}^{x}}-{2}^{x}$ |
3.在空间直角坐标系中,点P(1,3,6)关于x轴对称的点的坐标是( )
| A. | (1,3,-6) | B. | (-1,3,-6) | C. | (-1,-3,6) | D. | (1,-3,-6) |
7.从字母a、b、c、d、e中任取两个不同的字母,则取到字母a的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
5.在正方形ABCD之内随机选取一点M到点D的距离小于正方形的边长的概率是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点$(0,\sqrt{3})$,离心率为$\frac{1}{2}$.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点$(0,\sqrt{3})$,离心率为$\frac{1}{2}$.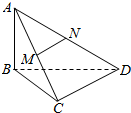 如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.