题目内容
已知函数f（x）=
，若|f（x）|≥mx，则m的取值范围是（ ）
|
| A、[0，2] |
| B、[-2，0] |
| C、（-∞，2] |
| D、[-2，+∞） |
考点：函数恒成立问题,分段函数的应用
专题：函数的性质及应用
分析：作出函数f（x）的图象，结合不等式恒成立，对m进行分类讨论即可得到结论．
解答：
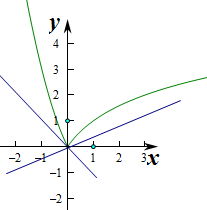解：作出函数f（x）的图象如图：若m=0，则|f（x）|≥mx成立，
若m＞0，由图象可知不等式|f（x）|≥mx不成立，
若m＜0，当当x＞0时，不等式|f（x）|≥mx成立，
要使|f（x）|≥mx成立，则只需要当x≤0时|f（x）|≥mx成立，
即|-x2+2x|≥mx，
即x2-2x≥mx，
则x2≥（m+2）x成立，
∵x≤0，
∴不等式x2≥（m+2）x等价为x≤m+2，
即m≥x-2恒成立，
∵x≤0，∴x-2≤-2，
即此时-2≤m＜0，
综上-2≤m≤0，
故选：B
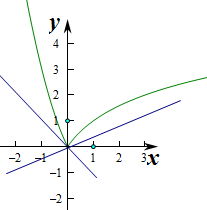解：作出函数f（x）的图象如图：若m=0，则|f（x）|≥mx成立，若m＞0，由图象可知不等式|f（x）|≥mx不成立，
若m＜0，当当x＞0时，不等式|f（x）|≥mx成立，
要使|f（x）|≥mx成立，则只需要当x≤0时|f（x）|≥mx成立，
即|-x2+2x|≥mx，
即x2-2x≥mx，
则x2≥（m+2）x成立，
∵x≤0，
∴不等式x2≥（m+2）x等价为x≤m+2，
即m≥x-2恒成立，
∵x≤0，∴x-2≤-2，
即此时-2≤m＜0，
综上-2≤m≤0，
故选：B
点评：本题主要考查不等式恒成立问题，利用数形结合以及分段函数的应用是解决本题的关键．
练习册系列答案
相关题目
已知向量
=（4，0），B是圆C：（x-
）2+（y-
）2=1上的一个动点，则两向量
与
所成角的最大值为（ ）
| OA |
| 2 |
| 2 |
| OA |
| OB |
A、
| ||
B、
| ||
C、
| ||
D、
|
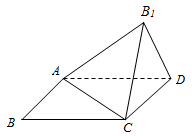已知四边形ABCD是矩形，BC=kAB（k∈R），将△ABC沿着对角线AC翻折，得到△AB1C，设顶点B1在平面ABCD上的投影为O．