题目内容
设
=x
+y
，且A、B、C三点共线（该直线不过端点O），则x+y等于（ ）
| OB |
| OA |
| OC |
分析：由点的共线可得存在一个实数λ，使
=λ
，转化为同一个起点的向量可得
=（1-λ）
+λ
，和已知的式子对照可得答案．
| AB |
| AC |
| OB |
| OA |
| OC |
解答：解：∵A、B、C三点共线，
∴存在一个实数λ，使
=λ
，
即
-
=λ（
-
）．
∴
=（1-λ）
+λ
．
又∵
=x
+y
，
∴x+y=（1-λ）+λ=1．
故选A
∴存在一个实数λ，使
| AB |
| AC |
即
| OB |
| OA |
| OC |
| OA |
∴
| OB |
| OA |
| OC |
又∵
| OB |
| OA |
| OC |
∴x+y=（1-λ）+λ=1．
故选A
点评：本题考查向量平行的判定，涉及向量的数乘的运算，属基础题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
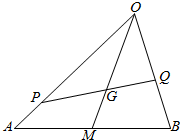如图，G是△OAB的重心，P、Q分别是边OA、OB上的动点，且P、G、Q三点共线．
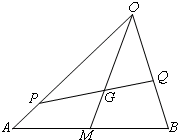如图，G是△OAB的重心，P、Q分别是边OA、OB上的动点，且P、G、Q三点共线．
如图，已知空间四边形OABC，其对角线为OB、AC，M、N分别是对边OA、BC的中点，点G在线段MN上，且